Q: Can we build a planet?

Posted on January 14, 2011 by The Physicist

Physicist: In theory, there’s nothing standing in the way.  In fact by constructing a planet from asteroids, comets, or dust you can expect to get a fair amount of energy back out.  Normally, you’d just chuck a bunch of dust, rocks, and ice together (the way God intended), but that releases a whole lot of heat, leaving the planet very molten for a very long time.

If instead you build a massive spherical scaffold around the future location of the planet you could lower new material gently to the surface, and generate power (e.g., tie a rope to the rock, and let it turn a generator as it falls).  So, if you do it right the whole thing would be “free” from an energy stand point.  In fact, you’d probably need some way to dissipate the extra unused energy.  The total energy, E, created by a planet as it coalesces from a dispersed cloud is approximately E = \frac{4 \pi}{5} G \rho^2 R^5, where \rho is the density, G is the gravitational constant, and R is the radius of the planet.  The energy ramps up very fast as R increases, so most of the energy comes from the end of the project.  So the good news is, you don’t have to have a molten planet, and there’s plenty of energy to be had.

Little history: that “R5” equation was derived to estimate whether or not Santa would destroy the world every year (He doesn’t).

The biggest concerns would be time scale, available materials, and whether or not you should bother.

Magrathea: the world building world.

I won’t even consider the question of engineering topography on the surface of the new world, since it’s not even a problem.  According to John Robert McNeill, as early as the 1980’s humankind became the greatest earth-moving force on the planet, surpassing everything else (erosion, volcanism, glaciers and rivers, and even ants and termites) put together.  So: shaping every mountain, valley, and ocean basin from the ground up (as it were)?  Doable.

Mines are big.

Time scale is a problem, of course, because it’s a big project.  The best way to gather materials at the construction site is to use other nearby planets for gravitational assists or “slingshots”.  After all, if you want to move a rock the size of a continent from place to place, the last thing you want to do is try to push it yourself with a rocket.  Instead you can nudge them slightly in the right direction and, within a couple hundred years, you’ve got your gigantic rock in the right place.  Later, when you’ve got enough of the planet built that it has its own gravity, and lowering material gains you plenty of energy, you can afford to attach super rockets to the asteroids and moons you want to include in your new planet.  Still, almost any reasonable construction scheme will have a very optimistic lower bound of at least several hundred years.

As for materials, the only information I have comes from our own solar system.  The Earth alone has more mass than 200 asteroid belts.  The closest source of material, not already in the form of planets and moons in our solar system is the Oort cloud, which (according to the best estimates to date) may contain enough material to make almost half a dozen Earths.  However, the Oort cloud is on the order of 10,000 AU away (1AU is the distance between the Earth and the Sun).  For comparison, the New Horizons probe, now en route to Pluto, is the fastest object ever made.  Despite that, it will still take about nine and a half years to cover the 30 AU out to Pluto (and NASA isn’t even going to have it slow down when it gets there).  To make things worse, almost all the mass out there is tiny grit.  You wouldn’t be grabbing rocks to send back, you’d be sweeping up fine space-powder and bagging it, one grain at a time.

So, say you don’t want to do that, and you decide to steal moons instead.  If you could somehow pull all of the moons of Jupiter out of orbit (using up most or all of your energy budget) you’d have enough material to create about 1/15 of one Earth.  The moral of this story is that once a solar system is formed it’s amazingly clean.  Other fully-formed star systems seem to be just about as clean.

So you may ask yourself: why bother?  Well, you probably shouldn’t bother.  Today is the golden age of planetary astronomy (and astronomy in general).  Over the past year we’ve found (and verified) about 1 to 2 new planets a week, around other stars.  518 have been found so far, and almost all of those have been within 300 light years.  It’s looking like there are hundreds of billions of planets in our galaxy at least, so it’s likely that whatever kind of planet you want, you could probably find it or simply adjust a planet that’s close enough.

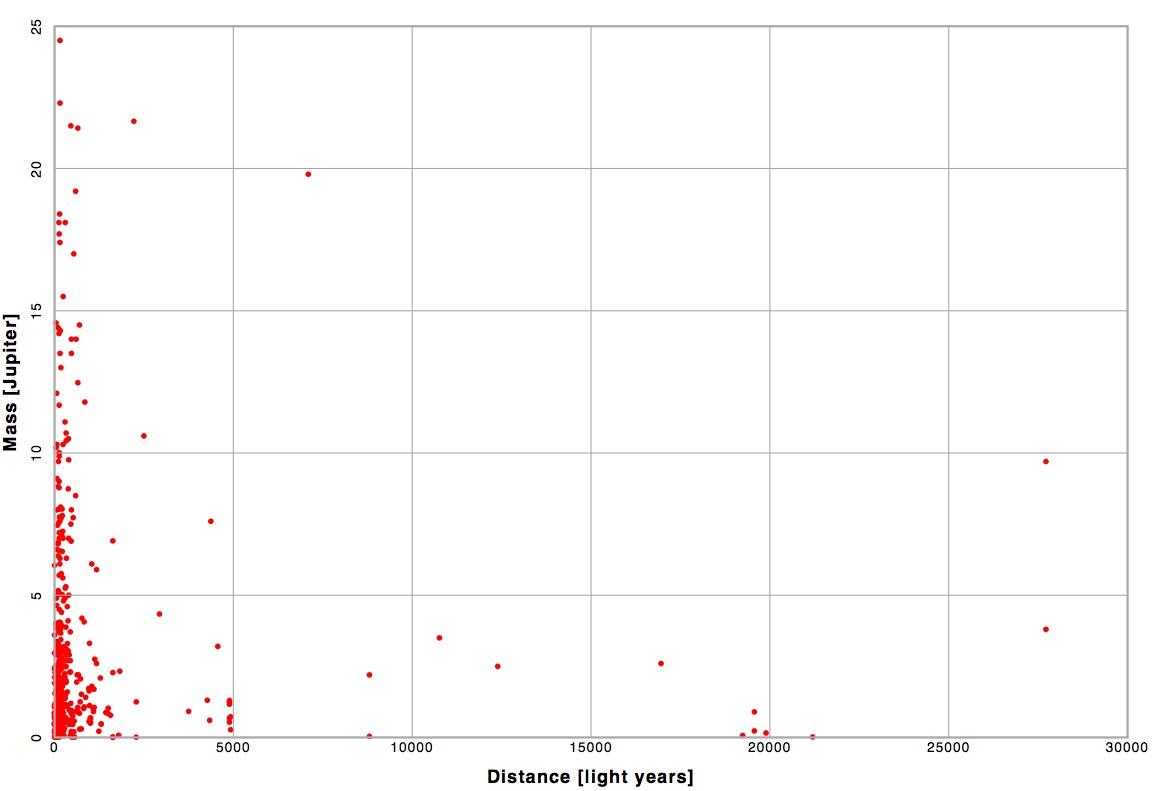
The mass and distance for all of the exoplanets found as of Jan. 14, 2011. If this plot included all of the missing planets it would be solid red. Click for full size.

After all, as long as we’re assuming that we can build planets from scratch, we may as well assume that we can just move to a distant star system.

Posted in -- By the Physicist, Astronomy, Physics | 30 Comments

Q: π = 4?

Posted on January 10, 2011 by The Physicist

Physicist: Recently this picture has been floating around confusing everyone, and making people think that maybe Indiana wasn’t completely off base when they moved to declare that \pi = 3.

The paradox. Approximating a circle with horizontal and vertical lines alone.

The exact answer to this question comes from deep in the field of mathematical analysis, which is where mathematicians go to think up worse-case scenarios.  That answer is long and uninteresting.  This answer is better.

This zig-zag path does approach the circle, so on the surface of it you’d expect that it would have the same length.  However, the length of a curve is more a function of it’s derivative (slope), and less a function of its position.  If you were to throw a jumbled up 20 foot rope into a 1 foot box, you wouldn’t say that the box is 20 feet across.  You’d want to straighten the rope out before you draw any conclusions.

To find the length of a curve you approximate it with lots of straight lines, then let the number of those lines go to infinity, and the lengths of the individual lines go to zero.

Using the Pythagorean theorem: (\Delta l)^2 = (\Delta x)^2 + (\Delta y)^2.  So if the total length of the curve is L, then by adding up all the little pieces you can get a good approximation:

L \approx \sum \Delta l = \sum \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sum \sqrt{\left[1 + \left(\frac{\Delta y}{\Delta x}\right)^2\right](\Delta x)^2} = \sum \sqrt{1 + \left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x

When the lengths get very small (that is, when \Delta l \to 0),  \Delta x becomes dx, \frac{\Delta y}{\Delta x} becomes \frac{dy}{dx}, and \sum becomes \int.  This is just a Riemann sum.

Now you have (one version of) the arclength equation: L = \int \sqrt{1+(\frac{dy}{dx})^2}\, dx!  Notice that the approximation has now become an equality.

If you were/are a calculus student, that “dy/dx” probably just set off some alarms in your head.  dy/dx is the “derivative of y with respect to x”.  If you were to make a graph of y vs. x, it would be the slope of the graph, and (this is the important part) L depends on it explicitly.

So finally, to answer the question, in order to approximate a path with another path, in such a way that they end up having the same length, you must be careful to make sure that the two paths have the same slope along their entire length.

As an aside: The “problem Archimedes?” thing is a reference to Archimedes’ approximation of \pi using polygons.  If you inscribe an N-gon (an N-sided polygon) into a circle, the length of it’s perimeter is: L = ND \sin{\left(\frac{\pi}{N}\right)}, where D is the diameter of the circle.

An inscribed 6-gon. Vocabuscenti may call it a "hexagon".

In this case, since the higher the number of sides the n-gon has, the better it approximates the circle both in position and slope, you’ll find that as N \to \infty, \frac{L}{D} = N \sin{\left(\frac{\pi}{N}\right)} \to \pi !  The \pi inside the Sine function falls out of the definition of “radians“, and basically boils down to the usual definition.

Posted in -- By the Physicist, Geometry, Math | 23 Comments

Q: How does a scientist turn ideas into math?

Posted on January 4, 2011 by The Physicist

The original question was:

How does a scientist/physicist map ideas and concepts into/onto mathematics?  Are there a sequence of steps?  If one starts with a mathematical model I can sort of see how using deduction, induction etc….

And what about the case where there is no mathematical model?  How does ideas concepts get from mind to math/formulas?  What is the “dirty work” that goes on behind the scenes?

Physicist: It’s hard to imagine most of the goings on in the world being turned into math.  Generally when “math” is brought up, most of us think of arithmetic, which really doesn’t do a whole lot on its own.  The majority of the interesting stuff in the world involves stuff much more fancy.  There’s already a lot of mathematical structures out there (calculus and topology and all kinds of stuff) so, when you can, you find one that’s familiar and see if it fits.  Otherwise you just create new maths.

 

Here’s how it starts: you tinker about with something until you notice a pattern.  Then you make up symbols that allow you to write down those patterns.  Then you see what the repercussions are.

For example: “***”, “ggg”, and “@@@”, all have something in common.  So, make up a symbol: “3”.  Make up some more symbols for other similar patterns and you’ve got the natural numbers: 1, 2, 3, 4, …

Now you can start making up symbols to describe all the reasonable things you can do with numbers: “+,-,\div,\times,\ldots“.  Boom!  Now you’re cooking with arithmetic!

2+3=5. Any questions you may have about the properties of "+" should be directed to the appropriate diagram.

Here’s where the abstraction starts.  New symbols come as part of a package that includes rules.  Generally by staring at the situation you can pull the rules out.  For example, by looking at the picture above you’ll notice that it doesn’t matter which group on the left side is first, so: 2+3=3+2.  Holy crap!  Commutativity!

Now you can start poking the rules to see how far they bend.  If they bend too far, you may find yourself in need of new symbols and rules.  For example: What happens if you subtract a larger number from a smaller number?  What if you add three or more numbers together instead of just two?  Keep up this line of questions and pretty soon you get parentheses, primes, rational numbers, all kinds of stuff.

As often as not, new ideas, symbols, and rules are created because they are needed, as opposed to being found (like the picture above).  For example: you can get from the natural numbers (1,2,3,..) to the rational numbers (2/3, 17/5, …) by merely asking some very reasonable questions about division.  But the rational numbers have “gaps” (like \pi and \sqrt{2}).  So now you need a number system with no gaps.  What do you do?  Make it up!  Call it the “real numbers”, \mathbb{R}.

What’s surprising, from a philosophical point of view, is that the rules that apply in one place apply in others.  Which is really nice, because then the rules and symbols that have been found in one area can immediately be applied in another.

Calculus, which only works on continuous things (like the real numbers), applies very well to describing fluid flow, despite the fact that fluids aren’t continuous (they’re made of atoms).  Even weirder; most quantum mechanical systems share a lot of properties in common with complex numbers.  So as QM was first being fleshed out it already had a couple hundred years of complex analysis to build on.

Don’t be deceived by the notion that the field of mathematics is dominated by numbers.  Keeping with the idea of 1) find a pattern, 2) make up a symbol and some rules, and 3) run with it: here are some other fields of math that have very little to do with numbers.

Geometry: That’s right, geometry.  It doesn’t really need numbers, it’s just taught that way.  You start with “two points make a line” and out pops about a thousand years of Greek history.

Algebra (group theory): This is the entirely abstract study of “there’s stuff, and things can happen to that stuff”.

Rubik's cubes: You can apply group theory to the arrangements of tiles, and how those tiles move.

To be more rigorous, and to actually get stuff done, it primarily considers “groups“, which have more structure than just “there’s stuff”.

Graph theory: The study of dots, and the lines that connect them.  If you’ve spent any time doodling, there’s a good chance you accidentally did some graph theory.  One simple result is: Any graph where every “vertex” has an even number of “edges” connected to it can be drawn completely without ever picking up your pen or repeating a line.

Starting anywhere on this graph you can draw the whole thing without lifting your pen, or repeating lines, because every vertex connects to an even number of edges.

This theorem is just another example of what happens when you start writing down patterns and rules, and following where they lead.

Topology: You usually hear about this in the context of “coffee mugs and donuts”.  This covers stuff like Mobius strips, and tori, to really weird stuff like projective planes.  Try this: take two Mobius strips and glue their edges to each other.  If you did it right you should have a Klein bottle.  Also, you can’t do it right because we don’t live in 4 or more dimensions.  Another result from the wide and weird world of algebraic topology!

Two examples of 2-D topology: "Costa's Surface" and a "Klein Bottle".

Logic: This includes stuff like: “If P, then Q” is equivalent to “If not Q, then not P”.  Surprisingly useful stuff, and it started with someone sitting down and making up rules and symbols (specifically: George Boole).  By the way, he would have written this last statement, “(P\Rightarrow Q)\Leftrightarrow (\bar{Q}\Rightarrow\bar{P})“.

Knot theory: Knot logic is logic nonetheless (suck on that, logicians!).  This is seriously alien math that takes the frustration of tangled string, and kicks it up a notch.  Knot theory also borrows some of the machinery from polynomials (despite having nothing to do with polynomials themselves) to form the various forms of knot polynomials.

The "Reidemeister Moves" from knot theory are an example of what passes for algebra over there. Ever twist or untwist a rubber band? Now it's got a name: R1.

So the point is: “turning something into math” just means writing down the patterns you see, and then pondering, for a while, the consequences of those patterns.  If there’s no readily available notation or symbols, make something up.  Let creativity be \mathcal{C}.

When “there’s no mathematical model” you either make one up, or you’re screwed.  But the rules you come up with really need to be solid.  For example, you could say “Let the quantity of love be L.  Love grows with time, therefore \dot{L}>0” (the time derivative of love is positive).  But this isn’t a well defined quantity, nor is this a hard and fast rule (You taught me well, Becky!).  You could create an entire mathematical system based on your lovsumptions (assumptions about love), but it won’t have anything to do with reality, or indeed love, if the rules aren’t solid.

Posted in -- By the Physicist, Math, Philosophical | 13 Comments

Q: Is Santa real?

Posted on December 24, 2010 by The Physicist

Physicist: The existence of Santa Claus is an established fact, beyond debate.  I, like most people of my generation, have verified his existence experimentally by means of the “Cookie test”.
The idea that millions of people, the world over, could leave cookies and milk out in the evening, and have them replaced by presents in the morning, without a “Jolly Agent” implies a conspiracy on a frankly Orwellian scale.  That “theory” can be dismissed out of hand.  Occam’s razor alone shows that this is essentially an open and shut case.

Santa Claus: Judgmental and Dutch.

NORAD (originally “CONAD”) has publicly tracked Santa’s sleigh since 1955.  According to A. Grawert, Esq. of Anonymous Law Firm LLP, although the consent of NORAD isn’t proof, it does provide a legal basis for his existence, as established in the landmark 1937 case “The People of the State of New York v. Kringle” (N.Y. Sup. Ct. 1937).
There is however a paranoid sub-culture of conspiracy theorists that quietly advocate the non-existence of Santa Claus (“asantists”).  So, for the rest of us, what follows is a look at some of the surprises of Cheer-based Gift-Delivery physics.

There are approximately 2 billion children in the world.  Assuming that there are 2 children per household and that the naughty and nice lists are the same length, then that leaves approximately 750 million households for St. Nick to visit.  Before the 24th, Santa’s Elves make toys and solve the Traveling Salesman Problem to plot the delivery route (Holiday magic and quantum computers are some of the only known methods for solving NP problems).  For a random arrangement of N points contained in a reasonably shaped, finite area, A, you can estimate the length of the optimal solution.  The length, L, is approximately L=\sqrt{\frac{NA}{2}}, and the average distance between houses is d=\frac{L}{N}=\sqrt{\frac{A}{2N}}.

Plugging in the non-Antarctic land area of the Earth (A=136,000,000 km2) and the number of Nice-list homes (N=1,500,000) yields L=200 million km and d=0.3 km.  Assuming that Santa covers the full distance in 24 hours, and spends half the time flying and half the time gifting and eating, he’d have an average speed of around 17,000,000 kph (or about mach 14,000), which is far less than the speed of light, and is totally doable.  He’d have to experience an acceleration somewhere in the ballpark of 30 billion g’s, on and off, for 12 hours, but again, that’s doable.

Even using so-called “conventional science” a human being can survive as much as 15 g’s when suspended in a fluid.  The highest acceleration survived by a human (a human named Col. John Stapp) is 46 g’s, and he was blind for barely a day.  But, keep in mind that rather than being a grouchy young human, Santa is in fact a jolly old elf.

Col. John Strapp: doing just fine.

It could be that what we think of as a “bowl full of jelly” may very well be an “elfin g-suit” that Santa uses to overcome the stresses of the journey.  The only way to say for sure is to ask him.  But, I’ve found empirically that almost every Santa you’ll meet is, in fact, an asantist impostor.

Traveling with an average speed of 17 million kph means that the back of Santa’s sleigh is in a hard vacuum.  More than that, the heat energy generated by Santa’s trip totals about 2 x 1015 tons of TNT equivalent, or about 40,000 metric tons of anti-matter (and 40,000 matching tons of ordinary matter).  “Conventional” physicists would say that the surface of the Earth would be completely vaporized by this joyous and welcome yearly Yule Tide.  What they don’t take into account is jingle-Bell’s theorem of quantum christmas, and a generous helping of X-mas miracles!

It would take about 5,000,000 Santa’s (or about 1022 tons of TNT) to completely destroy (disassemble) the Earth.  2 x 1015 tons of TNT would just throw the top half mile or so into space.  Happy holidays!

Update: Some concerned readers pointed out that the “# of naughty = # of nice” estimate may involve more optimism than is entirely warranted.

Which raises the question: given that Santa exists, and so does life on Earth, how many nice children can there be?  I bet a 1°C increase in the world temperature could be small enough to go unnoticed.  So (using the same estimates to back solve), if Santa’s break-neck course only released enough energy to cook the Earth by 1°C, then there can be no more than around 4,000 nice-households in the world.

It would seem that we can safely say that 99.9997% of children should have watched out, they shouldn’t have cried, they shouldn’t have pouted, and we can derive why.

Posted in -- By the Physicist, April Fools, Paranoia, Physics | 14 Comments

Q: Why isn’t the shortest day of the year also the day with the earliest sunset?

Posted on December 15, 2010 by The Physicist

The original question was: Hopefully you can help me to explain this mystery. I live in the northern hemisphere, in the U.S. I notice that winter solstice is the day with the shortest period of sunlight BUT it is not the day when the sun sets earliest. That day is around December 10th. So, the sun is already starting to set later every day even though we’re not yet at the winter solstice. Of course, the sun is rising more later to more than make up for the later sunsets so the days are still getting shorter for the next 8 or 9 days. I tell my friends that the sun is already starting to set later but they don’t typically believe this even though I’ve verified it on several web sites that compute sunrise/sunset.

My question is why isn’t the shortest day of the year also the day with the earliest sunset? There’s some asymmetry somewhere!

Physicist: “Asymmetry” is the perfect way to say it.
As the Earth moves around the Sun it needs to turn slightly more than 360 degrees to bring the Sun to the same place in the sky, because during the course of that day the Earth has also moved about 1 degree in it’s orbit (360 degrees over 365 days), which puts the Sun about 1 degree away from where it “should” be.

24 hours is not the time that it takes for the Earth to turn once (that’s 23 hours and 56 minutes). 24 hours is the average time it takes for the Sun to get back to the same place in the sky.  As seen from above the north pole, the Earth both turns on its axis and orbits the Sun counter-clockwise.

This discrepancy is the source of the difference between “standard” and “sidereal” days (the time it takes Earth to physically rotate exactly once).
The standard 24 hour day isn’t quite the time from noon to noon (solar day).  It’s actually the average noon-to-noon time (averaged over the year). That average time is set in stone, and it’s the time your watch reads.  After all, with most clocks today accurate to within a couple minutes a year, it’s easier to not set your clocks by the Sun, and just let them run.

However, because the Earth’s orbit is elliptical, the angle we cover every day in our orbit changes.  When we’re farther, the angle doesn’t change as fast, and the solar time gets a little ahead of standard time.  When we’re closer, the angle changes faster and the solar time falls a little behind standard time.

When we’re farther from the Sun the angle we sweep out is smaller, and the Sun falls behind our clocks (this is cumulative), so it rises and sets behind schedule. When we’re closer, the opposite occurs.

It so happens that the closest we get to the Sun corresponds with the Winter solstice (in the north), but not exactly.  The “perihelion” falls around January 4th, and the solstice falls around December 21st.

Solar time falls behind more and more between November and February (losing the most time on Jan. 4) thus pushing the sunset later.   The length of the day gets shorter up until Dec. 21 (pushing the sunset earlier).  The strength of these effects just happens to balance around December 10th (give or take), before that the length of the day is more important, and afterward the standard/solar time discrepancy is more important.

You don’t have to trust me. Set up a camera (anywhere on Earth) and take pictures of the sky at the same time everyday. The image on the right was made by a guy who did exactly that (http://www.perseus.gr/Astro-Solar-Analemma.htm).

The effect is pretty small, so in general the length of the day is the only thing you’d need to worry about (solar time never gets more than 15 minutes away from standard time).  When standard time became standard, sundial makers started putting an analemma (the picture above) on their sundials so people could correct for the difference.

Anyway, tell your friends you’re right!

Mostly unrelated tangent!: The seasons and the length of the day are caused by the tilt of the Earth’s axis.  The fact that the north points away from the Sun at about the same time that the Earth is closest to the Sun is a coincidence.  This leads to slightly less extreme seasons in the northern hemisphere.  When the axis tilts away in the north at the same time that the Earth is farthest from the Sun, the seasons in the north are slightly more extreme.  This leads to more snow cover.  And since the north has more land (where snow cover happens) more sunlight is reflected back into space (snow is white), which cools the planet more, which helps lead to ice ages.

Also, the Earth’s axis “wobbles” in a circle over the course of about 26 thousand years.  So, for example, in about 13 thousand years, the north will point away from the sun when the Earth is farthest away.  As a result, glacial periods have cycles of around 26 thousand years (or multiples).  Also as a result, the North Star has not been, and will not be, the North Star for long.  So soak it up.  Ancient Egyptians had to average between two stars, like savages.

Also!: The exact shape of the analema is a function of the tilt of the axis, the timing of the solstices and equinoxes, the eccentricity (“ellipticalness”) of the orbit, and the timing of the closest and farthest points in the orbit.  As such, the other planets each have their own analemas.  We can easily calculate what those should look like, but, with the exception of Mars, it’s unlikely we’ll be able to photograph them any time soon.  You can’t land a probe on the gas giants, you can’t see the sky on Venus, and stuff of Mercury tends to melt.

The analemma of Mars: the position of the sun photographed at the same time every few days for a year, as seen from the surface of Mars.  Specifically from the landing site of the Pathfinder mission.

Posted in -- By the Physicist, Astronomy, Physics | 17 Comments

Q: Why does “curved space-time” cause gravity?: A better answer.

Posted on December 11, 2010 by The Physicist

Physicist: The original post is here.

The curvature of space alone has almost no effect on the movement of objects until they are moving really fast.  With the exception of only the most extreme cases (black holes), space is very, very close to flat.  For example, the total stretching of space due to the Earth amounts to less than 1cm.  The precession of Mercury’s orbit is another example of the tiny effect of the curvature of space (and it is tiny).  Literally, there’s a little more space near the Sun than there “should” be, and as a result the direction in which Mercury’s orbit is elliptical moves.  It takes a little over 3 million years for it to go full circle.

In almost all cases the vast majority of an object’s movement is tied up in its forward movement through time. The curvature of spacetime (not just space) is responsible for gravity. Literally, near heavy objects, the “future direction” points slightly down. So anything that moves forward in time will find its trajectory pointing down slightly.  This takes the form of downward acceleration. This acceleration (time pointing slightly down) is entirely responsible for the motion of the planets, and every other everyday experience of gravity.

In flat space traveling forward in time has no effect on your movement through space. In curved space (e.g., near a large blue mass) parallel lines can come together, and moving through time leads to movement downward.

It may seem a little confusing that, once you’re moving, the explanation doesn’t change and falling is still caused by movement through time.  Well, there is some effect caused by spacial movement and the spacial part of the curvature, but these effects are almost completely overwhelmed by the effects from the time component of the velocity (much, much bigger).

Posted in -- By the Physicist, Mistake, Physics, Relativity | 123 Comments