Q: According to relativity, two moving observers always see the other moving through time slower. Isn’t that a contradiction? Doesn’t one have to be faster?

Posted on December 6, 2010 by The Physicist

Physicist: They definitely both experience time dilation.  That is to say, they both see the other person moving through time slower (you will always see your own clock running normally, in all circumstances).  The short resolution to the “paradox” is: if you’re flying past each other, and never come back to the same place again to compare clocks, what’s the problem?  You may both observe the other person’s clock running slower, but that’s not a contradiction in any “physical sense”.

Of course if you do meet up again, then you’ve got the “twin paradox”, which still isn’t a problem (or a paradox).  One of the most frustrating things about the universe is that there is no such thing as “absolute time“, which would allow you to say “who’s right”.  If you could ask the universe “what time is it?” the universe’s best answer would be “that depends on who’s asking”.  The universe is kind of a smart ass.

There’s a halfway decent explanation of the twin paradox here: “Q: How does the twin paradox work?” and there’s a quarterway decent, possibly simpler, explanation of why movement makes time pass slower here: “Q: Why does going fast or being lower make time slow down?“.  Personally, I think the question of this post is far more profound.

I should note here that the language physicists use makes the situation sound subjective; “the observer sees…”, “the person experiences…”, etc.  However, none of the effects (covered in a minute) are due to observer based effects, like the delay caused by the time it takes light to get from place to place.  Everything here is literal and physically real.

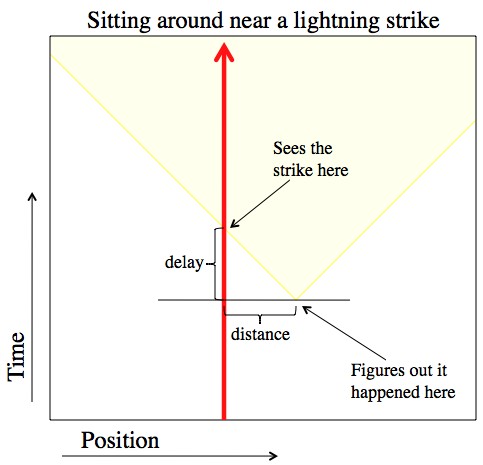
You don’t see an event when it happens, you see it when the light from the event gets to you. But you can easily figure out when it did happen by dividing the distance to the event by C, giving you the time delay.

This diagram is pretty standard physicist fare.  If you want to draw a picture of something happening in 4 dimensional spacetime, you just drop two of the spacial dimensions.  So here, time is up, space is left/right, the red arrow is a person (it doesn’t have to be a person) sitting still and moving forward in time (like you’re doing right now, in all likelihood).  The yellow triangle is a lightning strike (at the bottom) and the light expanding out from it.  The picture should make sense; the longer after the lightning strike (the higher on the picture) the farther the light from the strike has traveled (wider to the left and right).  “Lightning” is a common example of an event, because it hits in a definite place at a very definite time.  Plus, (spoiler alert) lightning is bright so, unlike most small instantaneous things, it makes sense that everyone should be able to see them.

Now let’s say you’ve got two people; Alice, who likes to hang out by the train tracks, and Bob, who likes to ride trains on said tracks.

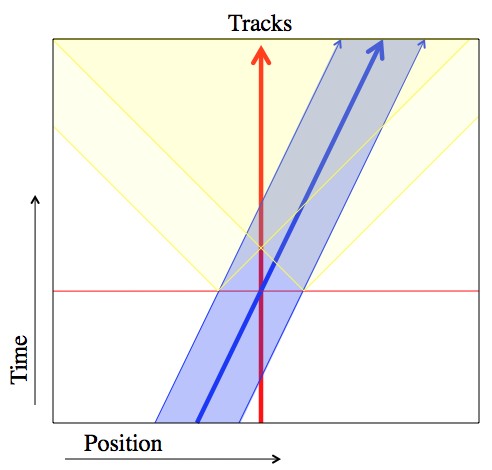
A train car (light blue) moves to the right. Right when Alice and Bob are eye-to-eye the front and back of the train car are hit by lightning. This moment, that Alice calls “Now!”, is the red line.

As the train, with Bob sitting in the exact center, passes Alice they high-five each other.  Suddenly, both ends of the train are struck by lightning.  Alice knows this because, very soon after the lightning strikes, the light from them get to her.  Being smart, she realizes that the strikes must have happened at the same time, because they happened equally far away from her, and the light took the same amount of time to get to her (see picture).  Moreover, really milking her cleverness, she predicts that Bob will see the lightning bolt at the front of the train first, and the lightning bolt at the back of the train second (see picture, some more).

The speed of light, C, is an absolute.  No matter where you are, or how fast you’re moving, C stays exactly the same.  So Alice’s reasoning is completely solid, and she’s right when she says that the lightning bolts happened at the same time.

When you say that two things are “happening at the same moment”, or “happening now” you’re saying that they’re on the same spacetime plane, that I’ll call a “moment plane”.  In the same way that a regular  2D plane is a big, flat subset of regular 3D space, the moment planes are big flat 3D subsets of 4D spacetime.

So the high five, the lightning strikes, and everything else in the universe at that moment, are all in the same “moment plane”.  However, that doesn’t necessarily mean that everything in that plane happens at the same time (although they do for someone, in this case Alice).

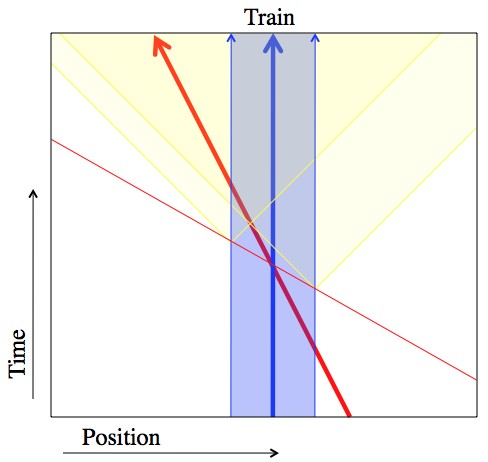
Same situation from the perspective of the train.  Bob sees the lightning at the front of the train first, and the lightning at the back of the train second, and can even figure out that Alice will see them at the same time.  However, he disagrees with Alice about when things happen.

Around 1900 the Michelson Morley experiment (among others) was demonstrating that the speed of light seemed to be the same to everyone, regardless of whether or not they’re moving.  Einstein’s great insight was “Hey everybody, if the speed of light seems to be the same regardless of the observers’ movement, then maybe it really is?”  He was a staggering genius.  Also, he was exactly right.

So, Alice was right about Bob seeing the front bolt first, and the back bolt second.  However, as far as Bob’s concerned, she was wrong about why.  Using the same reasoning Alice did, he figures that the speed of light is fixed (whether or not you’re moving), and the distance from him to the front and back of the train is the same, so since he saw the front bolt before the back, it must have happened first.  And he’s right.  Moreover, he thinks that the reason that Alice saw both at the same time is that she’s moving to the left, away from the first bolt and toward the second (picture).

The first thing that most people say when the hear about the train thought experiment is “Isn’t the person on the tracks correct, since they really are sitting still?”  Nope!  The tracks may be bigger, but (as Dr. V. E. Kilmer discovered experimentally) there’s no physical way to say who’s moving and who’s not.

Both Alice and Bob are completely correct.  What’s very strange is that the ideas we intuitively have about “nowness” are wrong.  As soon as two people are moving with respect to each other, the set of points that they consider “now” are no longer the same (different moment planes).  Alice’s “now” is the same red line above, but Bob’s sees it as “tilted”.

After all of that, what you should take away is: “a thing’s moment planes tilt up in the direction of its movement” (picture above).  If this is the first time you’ve seen this sort of stuff, you shouldn’t really believe any of it.  Or at least, you shouldn’t have internalized it.

This stuff isn’t terribly complicated, but it is really mind-bending, so take a moment.

Physically tilted “nows” are difficult to wrap your mind around. To encourage the reader to pause or go back a little bit; consider the above.

Finally, to actually answer the question, imagine the situation from the point of view of someone in between Alice and Bob, who sees them flying off at equal speeds in opposite directions.  This puts Alice and Bob on equal footing, and there’s no questions about “who’s right” or “who’s moving”.

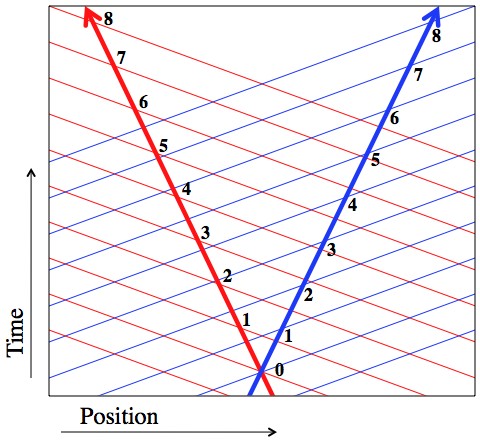
Alice and Bob’s now planes at various times.  If you were to ask Alice “how much time has passed for Bob now?” the answer will always be “less time than for Alice.”  The situation with Bob is exactly symmetrical.

Since the moment planes of each person “tilt up in the direction of movement”, each person is always trailing behind the other in time.  When they pass each other they each start their stopwatches.  For that one moment they can agree that T=0 for both of them.  But that’s where the agreement ends.  If you ask Bob about what set of points in the universe (both position and time) correspond to T=7, he’ll have no trouble telling you.  Specifically, he’ll tell you “right now my stopwatch reads ‘T=7’ and, F.Y.I., Alice’s stopwatch reads ‘T=5′”.  Bob recognizes that this is because her clock is running slower, and he’s right.  At least, he’s right in terms of how time is flowing for him.

If you were to run over to Alice at the moment that her stop watch reads 5 (using a TARDIS or something), she would say “right now my stopwatch reads ‘T=5’ and Bob’s reads ‘T=3.5′”.  Also being clever, she realizes that this is because Bob’s clock is running slower, and she’s right.  Notice she doesn’t say “T=7”.  Once again, this is because they disagree on what “now” means, since their moment planes aren’t the same.

The first question that should be coming to mind is something like “Well, what’s really happening?” or “How is time actually passing?”.  Sadly, time is a strictly local phenomena.  How it flows is determined (defined really) by relative position and relative velocity.  That is to say, there is no “universal clock” that describes how time passes overall.  The only reason that there seems to be some kind of universal clock is that we (people) are all moving at very nearly the same speed.  Or equivalently, we’re all sitting still in very much the same way.  Our time, length, and speed scale are all just too small.

Posted in -- By the Physicist, Philosophical, Physics, Relativity | 43 Comments

Q: What does 0^0 (zero raised to the zeroth power) equal? Why do mathematicians and high school teachers disagree?

Posted on December 4, 2010 by The Mathematician

Clever student:

 

I know!

x^{0} =  x^{1-1} = x^{1} x^{-1} = \frac{x}{x} = 1.

Now we just plug in x=0, and we see that zero to the zero is one!

Cleverer student:

 

No, you’re wrong! You’re not allowed to divide by zero, which you did in the last step. This is how to do it:

0^{x} = 0^{1+x-1} = 0^{1} \times 0^{x-1} = 0 \times 0^{x-1}= 0

which is true since anything times 0 is 0. That means that

0^{0} = 0.

Cleverest student :

 

That doesn’t work either, because if x=0 then

0^{x-1} is 0^{-1} = \frac{1}{0}

so your third step also involves dividing by zero which isn’t allowed! Instead, we can think about the function x^{x} and see what happens as x>0 gets small. We have:

\lim_{x \to 0^{+}} x^{x} = \lim_{x \to 0^{+}} \exp(\log(x^{x}))

= \lim_{x \to 0^{+}} \exp(x \log(x))

= \exp( \lim_{x \to 0^{+} } x \log(x) )

= \exp( \lim_{x \to 0^{+} } \frac{\log(x)}{ x^{-1} } )

= \exp( \lim_{x \to 0^{+} } \frac{ \frac{d}{dx} \log(x) }{ \frac{d}{dx} x^{-1} } )

= \exp( \lim_{x \to 0^{+} } \frac{x^{-1}}{- x^{-2}} )

= \exp( \lim_{x \to 0^{+} } -x )

= \exp( 0)

= 1

So, since  \lim_{x \to 0^{+}} x^{x} = 1, that means that 0^{0} = 1.

High School Teacher:

 

Showing that x^{x} approaches 1 as the positive value x gets arbitrarily close to zero does not prove that 0^{0} = 1. The variable x having a value close to zero is different than it having a value of exactly zero. It turns out that 0^{0} is undefined. 0^{0} does not have a value.

Calculus Teacher:

 

For all x>0, we have

0^{x} = 0.

Hence,

\lim_{x \to 0^{+}} 0^{x} = 0

That is, as x gets arbitrarily close to 0 (but remains positive), 0^{x} stays at 0.

On the other hand, for real numbers y such that y \ne 0, we have that

y^{0} = 1.

Hence,

\lim_{y \to 0} y^{0} = 1

That is, as y gets arbitrarily close to 0, y^{0} stays at 1.

Therefore, we see that the function f(x,y) = y^{x} has a discontinuity at the point (x,y) = (0,0). In particular, when we approach (0,0) along the line with x=0 we get

\lim_{y \to 0} f(0,y) = 1

but when we approach (0,0) along the line segment with y=0 and x>0 we get

\lim_{x \to 0^{+}} f(x,0) = 0.

Therefore, the value of \lim_{(x,y) \to (0,0)} y^{x} is going to depend on the direction that we take the limit. This means that there is no way to define 0^{0} that will make the function y^{x} continuous at the point (x,y) = (0,0).

Mathematician: Zero raised to the zero power is one. Why? Because mathematicians said so. No really, it’s true.

 

Let’s consider the problem of defining the function f(x,y) = y^x for positive integers y and x. There are a number of definitions that all give identical results. For example, one idea is to use for our definition:

y^x := 1 \times y \times y \cdots \times y

where the y is repeated x times. In that case, when x is one, the y is repeated just one time, so we get

y^{x} = 1 \times y.

However, this definition extends quite naturally from the positive integers to the non-negative integers, so that when x is zero, y is repeated zero times, giving

y^{0} = 1

which holds for any y. Hence, when y is zero, we have

0^0 = 1.

Look, we’ve just proved that 0^0 = 1! But this is only for one possible definition of y^x. What if we used another definition? For example, suppose that we decide to define y^x as

y^x := \lim_{z \to x^{+}} y^{z}.

In words, that means that the value of y^x is whatever y^z approaches as the real number z gets smaller and smaller approaching the value x arbitrarily closely.

[Clarification: a reader asked how it is possible that we can use y^z in our definition of y^x, which seems to be recursive. The reason it is okay is because we are working here only with z>0, and everyone agrees about what y^z equals in this case. Essentially, we are using the known cases to construct a function that has a value for the more difficult x=0 and y=0 case.]

Interestingly, using this definition, we would have

0^0 = \lim_{x \to 0^{+}} 0^{x} = \lim_{x \to 0^{+}} 0 = 0

Hence, we would find that 0^0 = 0 rather than 0^0 = 1. Granted, this definition we’ve just used feels rather unnatural, but it does agree with the common sense notion of what y^x means for all positive real numbers x and y, and it does preserve continuity of the function as we approach x=0 and y=0 along a certain line.

So which of these two definitions (if either of them) is right? What is 0^0 really? Well, for x>0 and y>0 we know what we mean by y^x. But when x=0 and y=0, the formula doesn’t have an obvious meaning. The value of y^x is going to depend on our preferred choice of definition for what we mean by that statement, and our intuition about what y^x means for positive values is not enough to conclude what it means for zero values.

But if this is the case, then how can mathematicians claim that 0^0=1? Well, merely because it is useful to do so. Some very important formulas become less elegant to write down if we instead use 0^0=0 or if we say that 0^0 is undefined. For example, consider the binomial theorem, which says that:

(a+b)^x = \sum_{k=0}^{\infty} \binom{x}{k} a^k b^{x-k}

 

where \binom{x}{k} means the binomial coefficients.

Now, setting a=0 on both sides and assuming b \ne 0 we get

b^x

= (0+b)^x = \sum_{k=0}^{\infty} \binom{x}{k} 0^k b^{x-k}

= \binom{x}{0} 0^0 b^{x} + \binom{x}{1} 0^1 b^{x-1} + \binom{x}{2} 0^2 b^{x-2} + \hdots

= \binom{x}{0} 0^0 b^{x}

= 0^0 b^{x}

where, I’ve used that 0^k = 0 for k>0, and that  \binom{x}{0} = 1. Now, it so happens that the right hand side has the magical factor 0^0. Hence, if we do not use 0^0 = 1 then the binomial theorem (as written) does not hold when a=0 because then b^x does not equal 0^0 b^{x}.

If mathematicians were to use 0^0 = 0, or to say that 0^0 is undefined, then the binomial theorem would continue to hold (in some form), though not as written above. In that case though the theorem would be more complicated because it would have to handle the special case of the term corresponding to k=0. We gain elegance and simplicity by using 0^0 = 1.

There are some further reasons why using 0^0 = 1 is preferable, but they boil down to that choice being more useful than the alternative choices, leading to simpler theorems, or feeling more “natural” to mathematicians. The choice is not “right”, it is merely nice.

Posted in -- By the Mathematician, Math, Philosophical | 1,177 Comments

Q: Can you do the double slit experiment with a cat cannon?

Posted on December 1, 2010 by The Physicist

Physicist: It helps to first get an idea of how the double slit experiment is done.  The double slit experiment works for any particle, but in what follows I’ll use light to avoid confusion.

Shine light on two slits separated by some distance d.  The light that emerges on the other side is free to scatter in any direction, but it doesn’t.  Instead we find that it prefers a particular set of angles, and that these angles depend on d and the wavelength of the light, \lambda.

In the picture below the upward angle means that the light from the bottom slit has to take a slightly longer path.  If the path difference is equal to a multiple of the wavelength, then the light from the two slits will be “in phase”, and will experience constructive interference.

Changing the angle changes the difference in path length from the two slits. When the difference is a multiple of the wavelength you get constructive interference.

It’s subtle, but already two assumptions have been made.  1) the screen that the light is being projected onto is very far away, so the light from the two slits, that gets to a particular point, follow roughly parallel paths.  This is a reasonable assumption, and doesn’t cause any problems.  2) the light that comes out of the two slits is already in phase, and has the same wavelength.  Luckily, there’s more than one way to skin a cat; either you use coherent (laser) light, or you make all the light come from a very small source (like another slit).

As a quick historical aside: When Thomas Young originally did this experiment he was looking at the interference pattern produced by allowing sunlight to pass through a colored filter (to get one \lambda), then a single slit (to get the light “coherent”), then the double slits, then projected onto a wall.  It was very dark, and (one can only assume) Young was very squinty.  Tom was about the smartest person ever to live.  He let the cat out of the bag for shearing forces, the Rosetta stone, and the transverse-wave nature of light, to name a very few.  He was the polymath cat that ate the canary of science.

Back in the day (1924) fat cat Louis de Broglie, the 7th duke of Broglie, proposed the idea (later proven experimentally) that not only is light a wave; everything is.  Kittens (the cute ones) have a mass of about 0.3kg, and old timey cannons have a muzzle velocity as high as the speed of sound (340 m/s).  This translates to a de Broglie wavelength of \lambda=\frac{h}{mv}\sqrt{1-\left(\frac{v}{c}\right)^2}=6.5\times 10^{-36}m.

Lambda = 6.5x10^(-36) m

Since kittens are about 0.1m long, the slits should each be about that size, and, say, 2m apart (larger slits need to be farther apart, to keep the interference fringes from overlapping).  So d = 2m.  Finally, you’d like the interference fringes on the screen to be several times farther apart than the kittens are large, otherwise you won’t be able to tell which kitten impact corresponds to which fringe.  Say 1m apart, give or take.

The smaller the wavelength, the closer the fringes are together, and the harder it is to tell that there are fringes at all.

The separation between fringes is approximately L\Delta \theta, where L is the distance to the projection screen, and \Delta \theta is the angle between two adjacent fringes.  For small angles you can use the aptly named “small angle approximation” for sine: \sin{(x)}\approx x, and you’ll find that \Delta \theta \approx \frac{\lambda}{d}.  Since I’d like the fringes to be at least 1m apart, 1 \approx L\Delta \theta \approx \frac{L\lambda}{d} and so L \approx \frac{d}{\lambda} = 3.1\times 10^{33}m.

So, after passing through (both) of the double slits the cats will have to fly through about 330 quadrillion light years of purfectly empty space, before impacting the projection screen (on their feet, naturally).  Unfortunately, the visible universe is just a hell of a lot smaller than that.  Even so, this cat-astrophe is not the biggest problem with the cat-based double slit device.

Not to con-cat-enate the difficulties, but the biggest problems stem from the supreme challenge of generating a “coherent cat beam” (a “cat-hode ray”, as it were).  Also, in order to get reasonable results from the experiment, it should be repeated at least 1036 times (about one hundred identical-to-the-last-atom-cats per fringe).  As a quick aside; that’s too many cats.

In order to do the double slit experiment, especially when tiny wavelengths are involved, it’s very important that all of the particles involved are exactly identical and in phase.  The best way to do this with light is to build a laser (which is an acronym for “Light Amplification by Stimulated Emission of Radiation”).  Light (being made of bosons) obeys Bose-Einstein statistics, and as such the presence of a bunch of identical photons increases the likelihood of new identical photons being generated (that’s not obvious, so take it as read).  Laser generation is an example of large scale entanglement, but unfortunately extending the technology to large scale cat entanglement would require all the yarn.

Coherent matter waves do exist, but so far they’ve all been made up of atoms in a Bose-Einstein condensate.  It’s true what they say; curiosity and picokelvin temperatures killed the cat.

A pulsed, coherent "atom-laser".

So to create a “caseo” (Cat Amplification by Stimulated Emission of Other cats), would require gathering so many exactly identical bosonic cats (“bosonic” here means an even number of protons, neutrons, and electrons), that the probability of new identical cats spontaneously forming from some kind of proto-cat particle soup becomes fairly high.  Getting a “cat field” with entropy that low (zero) would be, I suspect, as difficult as herding cats.

But, if you can do that, then you can create a coherent cat-beam of absolutely identical cats.  And once the 330 quadrillion light year long double slit apparatus is set up, you’re ready to go!  Easy peasy!

No point in pussy-footing around it, there’s a reason why we don’t see quantum mechanical effects in “every day life” (with a few exceptions).

Posted in -- By the Physicist, Physics, Quantum Theory | 23 Comments

Q: How is the “Weak nuclear force” a force? What does it do?

Posted on November 25, 2010 by The Physicist

The original question was: I keep reading on the internet about how it’s the electromagnetic force which causes positive and negative charges and their reactions, it is gravity which pulls all matter together, and it’s the strong nuclear force which pulls quarks together. What is it that the weak force does though? I have read that it “governs” radioactivity, but what does that mean? What is its purpose?

Physicist: The short answer is that the W and Z bosons (the Weak interaction carriers) really don’t “fit” anywhere else.  And, although it’s not the most important thing it does, the W and Z bosons do carry momentum, which is all that a force really has to do at the end of the day.
The big difference is that the other force carriers; photons, gluons, and (if they exist) gravitons, leave the involved particles alone (other than energy and momentum).  They’re very “clean” interactions.  While the Weak force can mediate interactions between particles without changing them (this is a result that helped point the way to the discovery of the “electroweak force”), it can also carry stuff with it, like charge.  By taking charge from one thing, and giving it to another, it’s changed the particles involved.  That last bit is important during “beta decay”, which is the type radioactive decay that the Weak force is involved in.

A muon and an electron neutrino exchange a W boson (carrying a negative charge, and some momentum), which changes the muon into a muon-neutrino and the electron-neutrino into an electron. This interaction is extremely rare. Far more common is muon decay, but that doesn't demonstrate the point.

Gluons can also cause the involved particles to change, specifically switching protons and neutrons.  However, if you start with one neutron and one proton, and you end with one neutron and one proton, what’s the difference?  The Weak force is the alchemist of the forces.

Posted in -- By the Physicist, Particle Physics, Physics | 7 Comments

Q: Does Gödel’s Incompleteness Theorem imply that it’s impossible to be logical?

Posted on November 24, 2010 by The Physicist

The original question was:
The question is in context with Kurt Gödel’s Incompleteness Theorem.

Question: If no formal logic can ever be, complete and consistent, does that mean, humans are illogical beings?

Further elaboration of the question:  Imagine a mathematician seeing a statement and intuitively knowing that the statement is true.  But the statement is unprovable.

Conclusion:  If the mathematician was a logical being, he would not be able to conclude that the statement is true.  Because it is unprovable.  But since he knows it is true, it must mean that the mathematician is an illogical being.  Because the mathematician doesn’t use logic to conclude – he use intuition.

Further clarification:  Since maths is based on axioms – which are statements that are true but unprovable.  Does this mean that the creator of the axioms is an illogical being?  Because the axioms would never exist if the creator was a logical being.

To take the question further:  Are humans constrained by logic in the sense that we could model the universe by a big equation, then calculate for a later given time, what the state of the universe is in?  So our actions would just be a product of a predefined mathematical path, which we don’t know (or might never know).

Or are humans not limited by logic so it would be impossible to model the universe by a big equation.
Because the equations ‘foundation’ is based on something which cannot ‘contain’ an equation for an illogical being?

I’m trying to hint on the question about: free will vs. fate.

Mathematician: Human beings are very, very far from perfectly logical beings (by which I mean that our thinking is often at odds with logic, and we routinely draw false conclusions by misprocessing information). There is no need to reference the incompleteness theorem to show that. Wikipedia’s list of fallacies does a nice job of cataloging many of the most common errors in thinking that humans make. I think it is very safe to assume that most people in the world have made at least a handful of the errors in this list, and everyone has made at least one of these errors at some point.

But, the fact that we are frequently illogical says nothing about whether human behavior could be predicted by applying the laws of physics to a detailed description of a human’s current state. It may be possible to make such a prediction in theory (though accuracy will be inherently limited by Heisenberg’s uncertainty principle, imperfections in our measurement tools, and other factors). In practice, however, predicting a person’s behavior using physics is absurdly difficult to do and it is possible that we will never come close to being able to do so. It is not inconceivable though that one day we will be able to model approximate human behavior in the short term by using a very detailed simulation of a person’s brain. At this point in time though, we can only speculate.

Physicist: The most frustrating thing about the Incompleteness theorem is not just that it shows that there are an infinite number of true and unprovable statements, but that it provides no means to figure out which statements those are.  We have a lot of statements that we assume (or define) to be true without proof, like “you can’t split a point”.  To make it sound as though there’s more to it than that, we call them “axioms”.  It’s not that they’re intuitively true, they’re defined to be true, and what we call logic follows afterward.  When a mathematician says something is “true” it’s always “true, given some set of axioms”.
As far as modeling the universe goes: The universe is, on one level, entirely deterministic.  If you had access to the total quantum wave function of the universe you could roll it forward in time (deterministically), no problem.  However, this isn’t how we experience the universe.  We only experience a tiny fraction of this wave function.

Basically, different versions of you experience every possible outcome of every event, so it no longer makes any sense to ask “which will happen?”.  They all happen (all that are possible), but each version only experiences one.  That isn’t terribly clear, but there’s a post about almost exactly this question here.

Posted in -- By the Mathematician, -- By the Physicist, Logic, Math, Philosophical | 28 Comments

Q: If accelerating charges radiate, and everything is full of charges, then why don’t I radiate every time I move?

Posted on November 20, 2010 by The Physicist

The original question was: From what I understand, an accelerating charged object will emit radiation (such as an accelerating electron). However, considering that our bodies consist almost entirely of charged particles, why is it not that we are constantly emitting electromagnetic radiation. Every time I move, say while typing this email, every electron in my arm is being accelerated. So, why am I not emitting a constant stream of radiation while doing so?

Physicist: There are a couple reasons; firstly, your charges are in balance, and secondly, a human can only move so fast.

Very nearly every electron in your body is right next to a positively charged nucleus. Every movement of a negative charge that would create a wave in one direction is coupled to an opposite wave created by a nearby positive charge.

Moving a charge makes a wave. Moving an opposite charge makes exactly the same wave, just oppositely. If the charges are right next to each other, these two waves cancel each other almost completely.

Since the charges are merely very close to each other, and not in exactly the same place, there are some very slight “near field” effects.  But that’s not radiation (radiation is sometimes called the “far field“).  Also, even if you built up a huge static charge (so that not every charge was balanced) the acceleration it would take to radiate a noticeable amount of energy would not be survivable.  The electrons in a radio tower regularly experience accelerations in excess of tens of million G’s.

Posted in -- By the Physicist, Physics | 8 Comments