Ask a Mathematician / Ask a Physicist

Q: What is the “monogamy of entanglement”?

Posted on October 26, 2018 by The Physicist

Physicist: The Monogamy of Entanglement is the statement that “maximally entangled” particles only show up in pairs. Entanglement is a sliding scale, so things can be non-entangled or a little entangled, but when the quantum states of two things are completely tied up in each other, there’s just no room for a third. This is more about how entanglement is defined mathematically and less about a dramatic insight into the true nature of reality.

Monogamy of Entanglement: Two maximally entangled particles cannot be entangled with any others. But the exact meaning of entanglement, like matrimony, is a matter of definition.

One particle: Quantum stuff can be (and generally is) in a “superposition”, multiple states at the same time. For example, an electron belonging to Alice (or anyone else), can be both “spin up” and “spin down” in equal parts; a superposition that’s written $|\uparrow\rangle_A+|\downarrow\rangle_A$ . Of course, you never look at something and notice that it’s in more than one state (superpositions need to be inferred using tricks like the double slit experiment). Before measuring its spin, the electron can be in the superpostion $|\uparrow\rangle_A+|\downarrow\rangle_A$ , but after measuring, its state is definite, either $|\uparrow\rangle_A$ or $|\downarrow\rangle_A$ (depending on what the result was). Which of these results you see is fundamentally random.

Now here’s the thing. Quantum randomness is relative. One person’s superposition is another person’s definite state. For example, that superposition from earlier is also a definite state $|\uparrow\rangle_A+|\downarrow\rangle_A=|\rightarrow\rangle_A$ . The spin right/left states are literally a superposition of the spin up/down states (this was as surprising and weird when it was first figured it out as it should be for you right now). If you measure $|\rightarrow\rangle_A$ in the vertical direction it’s a superposition of spin up and down, but if you measure it sideways it’s a definite state.

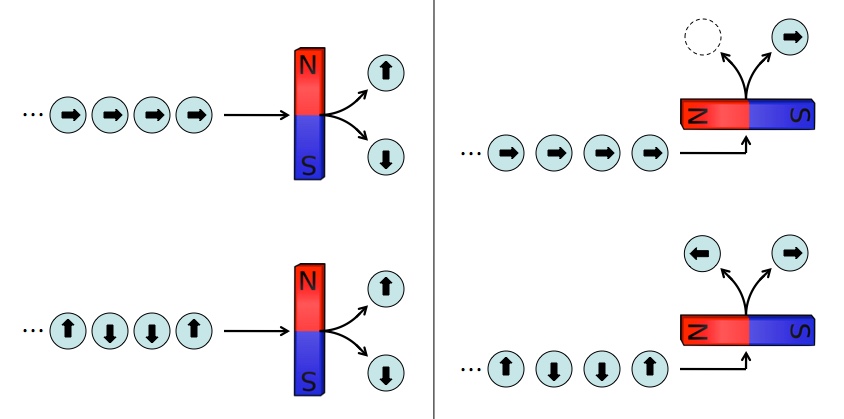
Spin causes particles to act like tiny magnets, which gives us a handy way to measure it. Left: When you measure spin vertically, there’s no way to tell the difference between a string of spin right electrons (top) and a string of random spin up/down electrons (bottom). Right: But if you measure horizontally, the string of spin right electrons always get sorted correctly, while the up/down electrons continue to produce random results.

If some devious ne’er-do-well sent you a never-ending stream of $|\uparrow\rangle_A$ or $|\downarrow\rangle_A$ states, flipping coins to determine which every time, it would look the same as a stream of $|\rightarrow\rangle_A$ states so long as you measured both vertically. But if you measured sideways, then the stream of $|\rightarrow\rangle_A$ states would always yield the same predictable result ( $|\rightarrow\rangle_A$ ), and the stream of random up/down states would still yield random results. In exactly the same way that the left/right spin states are superpositions of the up/down states, the up/down states are superpositions of the left/right states (so they produce random results when measured horizontally).

Here’s the point. If you’re always looking at the same, definite state, then you should be able to find some measurement that always produces a definite result. But if you’re being fed a random set of states, there’s no way to do a measurement that produces consistent results. I suppose you could turn the detector off and walk away, but that’s dirty pool.

Quick aside: I’m dropping the coefficients in front of the states that would normally dictate their probability of being measured (the state $|\uparrow\rangle_A+|\downarrow\rangle_A$ where both results show up 50% of the time, should have been written $\frac{1}{\sqrt{2}}|\uparrow\rangle_A+\frac{1}{\sqrt{2}}|\downarrow\rangle_A$ ). I figure if you notice they’re missing, then you probably already know how to put them back, and if you don’t notice they’re missing, then you probably don’t want to be distracted.

Two Particles: When you need to worry about multiple systems (particles, quantum computers, needlessly diverse collections of scarves, or whatever else), you don’t worry about their individual superpositions of states, you worry about superpositions of their collective states. So if you have a second electron, under the custodianship of Bob, you wouldn’t first talk about the states of Alice’s electron ( $|\uparrow\rangle_A$ and $|\downarrow\rangle_A$ ) and then, having done that, talk about the states of Bob’s electron ( $|\uparrow\rangle_B$ and $|\downarrow\rangle_B$ ). Instead, you’d talk about superpositions of their collective states ( $|\uparrow\rangle_A|\uparrow\rangle_B$ , $|\downarrow\rangle_A|\uparrow\rangle_B$ , $|\uparrow\rangle_A|\downarrow\rangle_B$ , and $|\downarrow\rangle_A|\downarrow\rangle_B$ ).

Left: In classical physics a system’s state is the aggregation of each part taken individually. Right: In quantum physics the system as a whole has a state that’s shared between each part.

For example, if both electrons are in the same equal superposition of spin up and down from earlier, then their collective state is

If Alice measures her electron and finds that it’s spin up, then the state of the pair is now

$|\uparrow\rangle_A\left(|\uparrow\rangle_B+|\downarrow\rangle_B\right)$

and if she finds that her electron is spin down, then the overall state is

$|\downarrow\rangle_A\left(|\uparrow\rangle_B+|\downarrow\rangle_B\right)$

In other words, in this situation it doesn’t matter what Alice sees; Bob’s state is independent of it. This particular collective state can be described first by considering Alice’s electron and then considering Bob’s (or vice versa), because knowing the result of a measurement on one part tells you nothing about what you’ll see when you measure the other. A state like this is called “separable”, because it can be separated mathematically. Physicists are very clever namers of things, which is why they often refer to themselves as namerators.

Non-seperable states are entangled; a measurement on one part gives you information about what the result of a measurement on another part will be. For example,

$|\uparrow\rangle_A|\uparrow\rangle_B+|\downarrow\rangle_A|\downarrow\rangle_B$

is definitely not separable. If Alice were to measure her electron the state of the system as a whole would be either $|\uparrow\rangle_A|\uparrow\rangle_B$ or $|\downarrow\rangle_A|\downarrow\rangle_B$

In other words, by looking at her own electron, Alice knows what Bob will measure, whenever he gets around to it. This state is “maximally entangled” because knowing one measurement allows you to perfectly predict the other.

But once Alice has measured her electron, and the system as a whole is now either $|\uparrow\rangle_A|\uparrow\rangle_B$ or $|\downarrow\rangle_A|\downarrow\rangle_B$ , then as far as Bob is concerned, his state is randomly either $|\uparrow\rangle_B$ or $|\downarrow\rangle_B$ . Unlike the single-particle case with $|\rightarrow\rangle$ , there’s no “correct” way to measure these randomly selected states to make the result definite.

This randomness isn’t a symptom of Alice having done a measurement, it’s a feature of entangled states in general. After all, Bob and his pet electron could be anywhere. Despite the nearly universal, but categorically false, belief that entangled particles affect each other, nothing that Alice does or doesn’t do with her electron will ever have any impact on Bob’s electron.

If Alice measures her particle, Bob gets a random result. But since the particles can’t communicate and it doesn’t actually matter what Alice does, Bob gets a random result anyway.

Entangled particles follow the same rule that single particles follow: wrong measurement = random result, correct measurement = definite result. But in order to do the “correct measurement” you always need to have access to the entire state. If you have both entangled particles in front of you, then you can easily do a measurement to determine which maximally entangled state you have (for example $|\uparrow\rangle_A|\uparrow\rangle_B+|\downarrow\rangle_A|\downarrow\rangle_B$ and $|\uparrow\rangle_A|\downarrow\rangle_B+|\downarrow\rangle_A|\uparrow\rangle_B$ are both maximally entangled, but very different states). These “correct” joint measurements always involve a step where the two particles are forced to interact, which is something you can’t do if they’re on opposite sides of the universe.

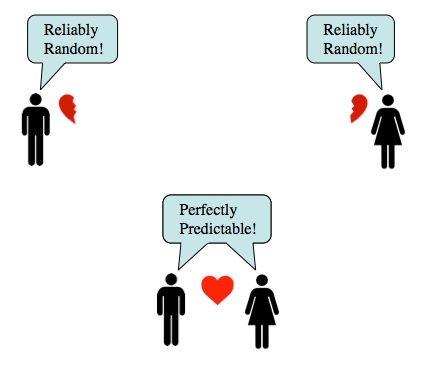
If you only have access to part of an entangled state, you’ll get random results no matter how you measure it. But if you have access to all of an entangled state, there is a “correct” measurement with predictable results.

This leads to a rather profound fact: entangled states always appear random when you only measure part of them. That is, they never seem to be in a superposition of states, they always appear to be a randomly selected state, since there’s no measurement that makes them predictable (see the one particle case).

There are still some clever things you can do with entangled particles that take advantage of their quantum correlations, like quantum teleportation, but two facts remain immutable: 1) when you measure one particle alone the result is random and 2) the two particles never ever influence each other in any way.

How entanglement is defined: When you don’t have access to both entangled particles and are forced to measure them one at a time, you get random results. You can describe how random those results are in terms of how much information it takes to describe them: two possible results (up or down) takes 1 bit of information (0 or 1). When you do have access to both entangled particles, you can do a measurement that will always produce the same, predictable result. One possible result takes zero bits of information. After all, if you had flipped a two-headed coin, would you really need to write down the results at all? Zero bits.

This difference between the randomness of the particles when they’re apart minus the randomness when they’re together is how entanglement is defined. A maximally entangled pair of particles has “1 ebit” of entanglement and a separable pair of particles has 0 ebits.

And yes, there are states in between. For example, $|\uparrow\rangle_A|\uparrow\rangle_B+|\uparrow\rangle_A|\downarrow\rangle_B+|\downarrow\rangle_A|\downarrow\rangle_B$ is partially entangled, because if Alice looks at her electron, she’ll learn a little about Bob’s electron (and vice versa), but not everything. This state has a modest 0.55 ebits of entanglement.

Three Particles: If Alice’s electron is in a superposition of spin up and down, its state is $|\uparrow\rangle_A+|\downarrow\rangle_A$ . If Alice and Bob each have electrons that are entangled such that they’re spin up and down together, then their state is $|\uparrow\rangle_A|\uparrow\rangle_B+|\downarrow\rangle_A|\downarrow\rangle_B$ .

So what’s stopping Carol and her electron from also being both spin up and down in tandem with Alice and Bob’s? Not a damn thing.

Today we can create states like this with not just three, but dozens of particles. No big deal. Any reasonable person (with at least a passing familiarity with quantum notation) would say that state looks pretty entangled.

With the third-act-introduction of Carol, suddenly they’re working with one of two randomly selected states ( $|\uparrow\rangle_A|\uparrow\rangle_B$ or $|\downarrow\rangle_A|\downarrow\rangle_B$ instead of a nice, pure, entangled state $|\uparrow\rangle_A|\uparrow\rangle_B+|\downarrow\rangle_A|\downarrow\rangle_B$ ). These states are random when Alice and Bob measure them on their own and when they bring their electrons together, they’re still looking at one of two random states, so even together the result of any measurement is going to end up random.

However! Entanglement is narrowly defined is in terms of how much more random your particles are when they’re apart vs. when they are together. Same amount of randomness means zero entanglement. So because there’s a third (or fourth or fifth…) party involved the state, no two parts can be maximally entangled.

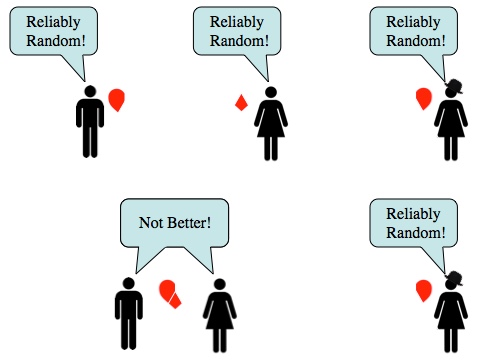
Entangled states are random apart and predictable together. That difference is how entanglement is defined. If a state is divided among more than two places, no pair can have the whole state, so the results are always random.

So it’s not that you can’t do fancy quantum states with many particles at once, and it’s not that something terribly profound happens when you move from using two particles to using three, but going by the stringent definition of entanglement: if two parties share a maximally entangled state with each other, they don’t share it with anyone else. One might even go so far as to say that entanglement is monogamous.

Like many seemingly arbitrary mathematical definitions, it turns out that the monogamy of entanglement is a powerful, useful statement. It is the key behind why quantum security is so secure (and quantum). By sharing a string of maximally entangled states with each other, then measuring some and sharing the results, Alice and Bob can check to see if there’s a third party corrupting their state. If there isn’t, they can dive into their private conversation. If there is, then they’ve caught themselves an eavesdropper. Quantum cryptography is Carol-proof!

Posted in -- By the Physicist, Equations, Math, Physics, Quantum Theory | 12 Comments

Q: Could dark matter actually be the “gravitational shadow” of parallel universes?

Posted on September 29, 2018 by The Physicist

Physicist: The very short answer is: nope. Well… almost certainly nope.

“Dark matter” is stuff that we can’t see or touch, but we know it exists because it affects the motion of regular matter, which we can see. Although there were vague hints that dark matter might be a thing going back about a century, it wasn’t until the 1970s that direct observations of the movements of stars in galaxies revealed the presence of too much matter. Way too much.

There’s so much more dark than regular matter in the universe, that its gravitational influence more or less dictates where the biggest concentrations of matter (galaxies and even galaxy clusters) end up.

By including dark matter in mathematical simulations, we get results that correspond well with the largest-scale distribution of matter in the universe, as well as the development of galaxies we see today.

One (possible) prediction of string theory is that our universe is a “brane“, a “sheet” of spacetime floating about in a higher dimensional space called the “bulk”. Other branes (other universes) might be floating around nearby, almost overlapping our universe, some small distance away. All of the particles native to a brane are stuck to it, but the gravity they produce might not be. So perhaps what we perceive as dark matter is really just the gravitation from matter in another nearby universe. That would explain why we don’t see it and why it doesn’t bump into things.

Artist’s interpretation of Brane Cosmology. Particles are stuck to branes (the sheets), which exist in a higher dimensional “bulk” spacetime (the back yard), but gravity from one brane can affect things in another. Maybe.

The danger of this line of thinking is that it requires taking several steps beyond the shelter of direct experimental evidence. The bulk, other branes, and even string theory itself are just a bunch of interesting ideas, since none of the theory’s novel predictions have been supported by experiment (so far).

Before delving into brane stuff, it’s worth considering what we know about dark matter. By carefully tallying up the number of stars, the distribution of their masses, the amount of gas and dust (by looking at how the local starlight filters through it), and then figuring out the amount of gravity due to all of it, we can figure out how fast each star in a galaxy should be orbiting said galaxy. We found two things: first, that there’s many times more matter in play than we can see and second, that this unseen matter is distributed around every large galaxy as though it had never been subject to accretion. That last bit is important.

Chunks of ordinary matter (orange) can bump into each other, causing them to slow down and concentrate in one place. Dark matter (grey) doesn’t bumping into anything, including itself, so it stays spread out.

Accretion is why stuff in space tends to clump together or flatten out into disks (or both!). When stuff has the option of bumping into itself, collections of matter go from incomprehensibly big, fluffy clouds, to concentrated pin-points (like stars and planets).

The four light-year tall Pillars of Creation form a tiny corner of the Eagle Nebula. This gas and dust is extremely spread out, but through accretion it concentrates a lot. If those pillars were each the size of Florida, the stars forming inside of them would be roughly the size of a piece of fruit.

By looking at the orbital speeds of stars vs. the distance to their galaxy’s cores we find that they are orbiting a disk of stuff as well as a diffuse cloud with around ten times the mass (the exact ratio varies from galaxy to galaxy). So whatever dark matter is, there’s lots of it and it doesn’t bump into anything.

The big difference between the 1970s and now is computer power, space telescopes, and the gradual muting of hairstyles. And nothing else. As our telescopes and computers improved slightly over the last few decades, we’ve been able to determine not just that dark matter exists, but where it exists and how much is around. Gravitational lensing bends light as it passes really heavy things. Determining the amount of mass in something based on how much it distorts the image of things behind it is something that’s very difficult to do with a slide ruler, but is pretty easy with a post-Pong-era computer.

A remarkable alignment of us (the camera), a galaxy (orange blurry thing), and a distant galaxy (smeared out blue ring). The gravity of the orange galaxy warps the image of the galaxy behind it.

If dark matter and regular matter show up in more or less the same place (which they usually do), then it’s difficult to tell the difference between the existence of dark matter and a misunderstanding of how gravity works. Luckily, dark matter is not only heavy but weakly interacting; a property that reveals itself when huge blobs of ordinary matter collide and their associated blobs of dark matter notably don’t.

The Bullet Cluster is actually a pair of colliding galaxy clusters. When galaxies or galaxy clusters collide their stars miss each other (because stars are stupid small compared to the distances between them), but their massive gas clouds find each other just fine. When they do, they heat up (not just from the physical impact but from being tossed around by their mutual magnetic fields) until they glow in the x-ray spectrum. Shining with x-rays makes these impacts stand out pretty clearly. So you’d expect that when galaxy clusters run into each other there should be a decent smearing of mass with a big chunk in the middle where the gas clouds pancake into each other. Instead, we see some hot gasses in the middle of the impact with the vast majority of the mass taking the form of two big chunks that cruised right through.

The Bullet Cluster is a collection of galaxies 3.7 billion light-years away (behind all the other galaxies and stars seen here). In this (very altered) picture the foreground galaxies are imaged in the visible spectrum (that’s actually what they look like), the pink blur is x-rays emitted by the colliding clouds of gas in the two clusters, and the purple is an overlayed map of matter density generated by analyzing gravitational lensing.

The point here is that dark matter is literal, actual stuff, not just a massively boneheaded mistake or miscalculation. You can point at where it is, say how much is there, and even talk about what it’s doing. We just can’t directly detect it because it doesn’t touch anything. As it turns out, that isn’t completely strange.

Different particles interact through different forces. For example, protons interact through all four fundamental forces: the strong nuclear force, the weak nuclear force, the electromagnetic force, and gravity. The strong force, keeps protons and neutrons packed tightly together in atomic nuclei. Electrons on the other hand interact through all but the strong force, which is why they buzz around the nucleus instead of being inside it.

Neutrinos only interact through the weak and gravitational forces. When you try and fail to walk through a wall, you’re interacting through the electromagnetic force. Without the electromagnetic force, neutrinos are free to pass right through damn near anything. On the order of a trillion pass through your body every second, and yet our best, biggest neutrino detectors only pick up a couple dozen a day (mostly from the Sun, and the detectors work both day and night since neutrinos don’t really notice the Earth). Since they interact through the weak force (and not very well) neutrinos are “weakly interacting”.

Whatever dark matter is, it seems to take things one step further: interacting through gravity alone. Without the strong force it wouldn’t form elements. Without the electromagnetic force it passes through ordinary matter and itself. And without the weak force we’re left with no way to directly detect it. But if there’s enough of it (and there seems to be), then we can detect its gravity.

Right now the search for dark matter is a little like setting out traps in your house because your cheese keeps going missing and you can hear skittering in the walls. There’s definitely something there and you know more or less where it is and what it’s like, but it would be nice to know exactly what you’re dealing with.

The search for dark matter: We know there’s something there, we’d just like to catch it to be sure.

So to actually answer that question from way back when: could dark matter be the gravity of stuff in another universe (or brane or whatever) bleeding into ours? Probably not. Dark matter doesn’t interact with ordinary matter, which could be because it’s on a different brane. But even so, based on how it gets distributed we know that it doesn’t interact with itself either. So bringing extra universes into play doesn’t answer any questions, it just muddies up an existing question with untested ideas. It’s like using honey to get gum out of your hair; the situation is different, maybe even thought provoking, but not better.

The mathematical model of the universe picture is from here.

The “brane” picture is from here.

The space stuff is all from NASA.

The chewed up wire picture is from here.

Posted in -- By the Physicist, Astronomy, Particle Physics, Physics | 31 Comments

Burning Man’s Mathematical Underbelly

Posted on September 21, 2018 by The Physicist

Physicist: I wrote an article about Burning Man and how Ask a Mathematician / Ask a Physicist started, that’s being featured over at Scientific American! Well worth a read, especially if you enjoy reading about what you’re reading.

Burning Man’s Mathematical Underbelly

Math and physics: standing room only.

Posted in -- By the Physicist | 4 Comments

Q: How was the number π first discovered? How did we first figure out it was 3.14…?

Posted on August 24, 2018 by The Physicist

Physicist: Unfortunately, the use of the number $π$ is older than recorded history so… who knows? But the use of $π$ at the beginning of recorded history wasn’t too sophisticated, so we can make guesses.

$π is the ratio of a circle’s circumference to its diameter. Everything about π boils down to that definition.$

Measure the distance around and across any circle, then divide, and you’ve got π.

The fact that the distance across a fixed shape is proportional to the distance around it is nothing special. The same is true for absolutely every shape. If you double the size of any shape, both the distance across and around will double as well, so their ratio stays the same.

Measure the distance around and across any square, then divide, and you’ve got 4.

Knowledge of the fact that the ratio of the circumference to the diameter of circles is some particular fixed number is older than recorded history. The fact that the ratio isn’t exactly three takes a little care and precision. Figuring out that the ratio has an infinite and non-repeating decimal expansion (that starts with 3.14159265358979323846264…) takes a little math and time.

A Babylonian tablet from around 4,000 years ago that declares the value of π to be 3. Could be worse.

If you can nail one end of a piece of string down and tie a quill or piece of charcoal to the other, then you can draw a damn-near-perfect circle. With a longer piece of string (at least 2π times as long, in fact) and a ruler, you can measure the circumference and as long as you’re careful, it’s pretty obvious that π≠3. As long as the error in your measurements is below 4%, you can tell the difference. The Babylonians created the Code of Hammurabi and some pretty impressive buildings, so presumably they could create a meter stick with centimeter marks (or rather, a kuš stick with šu-si marks). It turns out the tablet in the picture above is really a “cheat sheet” for roughly approximating the area of circles. They were known to have used $\frac{25}{8}=3.125$ , an approximation within half a percent of the correct value. Which, for the bronze age, is fine.

Since π shows up practically anytime you’re doing math involving circles, there were a heck of a lot of opportunities for people in the ancient world to notice it and we can’t be sure which first caught their eye (this is the drawback of discoveries that are older than history). For example, the volume, v, of a barrel with height h and diameter d is $v=\frac{\pi}{4}hd^2$ . If you want to predict how much water a cylindrical barrel can hold to within a couple percent, then you need to know π to at least a couple digits.

All of this is to say that π, while full of mathematical mysteries or whatever, is not some abstract idea. It’s something you can physically measure. Well… you can tell it’s not three anyway. The larger the circle and the better your measurements, the more digits of π you can discover, but the law of diminishing returns kicks in faster than an all-you-can-eat-week-old-sushi buffet.

By the time you know π out to N digits, you know the ratio of the circumference to the diameter of a circle to on the order of 1 part in 10^N. For example, if you know that π≈3.14, then you can fit a bike tire onto a rim to within a cm. If you know that π≈3.1415, you can build a fence around a circular acre to within a cm. And if you know that π≈3.1415926535, you can wrap a cable around the Earth with less than a cm of wasted cable. Arguably, knowing π out to ten or more digits is aggressively pointless, but that has never stopped mathematicians from practicing their cruel craft. Not once.

The definition of π not only gives us a recipe for physically measuring it, but also hundreds of ways to mathematically derive it, and that’s where the real precision comes from. Mathematicians like Archimedes and Liu Hui, and some nameless Egyptian a couple millennia before them, were able to approximate π using polygons. Liu Hui calculated π accurately out to three digits, a record slightly better than Archimedes’, that held for about a thousand years. Which is strange.

During the Roman siege of Syracuse, general Marcellus ordered that Archimedes should be captured alive because clever knows no nation. Unfortunately, geometry-ing to the very end, Archimedes was a jerk to the very first Roman he met.

Either Archimedes and/or historians really dropped the ball, or people in ancient Greece were more level-headed about knowing lots of digits of π than we are today. For a given circle, the points on an “inscribed polygon” touch the circle (so it’s inside) and the middle of the edges of a “circumscribed polygon” touch the circle as well (so it’s outside). Archie approximated π by inscribing and circumscribing 96-gons in and around the circle and calculating their perimeters. An inscribed polygon gives a lower bound, and a circumscribed polygon gives an upper bound, for the value of π. But here’s the thing: Archie didn’t just find the perimeter of 96-gons, he invented an iterative algorithm to calculate the perimeter of 2n-gons given n-gons. That is, he started with hexagons (6-gons) and bootstrapped up to 12-gons, 24-gons, 48-gons, and then inexplicably stopped at 96-gons. Evidently he had better things to do than calculate more digits of π. Which, to be fair, is not a high bar. He may have just declared the problem solved, since anyone following his procedure could find as many digits as they’d want, and moved on to heat rays or something (seriously, dude tried to build a solar heat ray to defend Syracuse).

Every time Archimedes’ iterative algorithm is used the estimate for π gets about 4 times better (its rate of convergence is 1/4). Which is less impressive than it sounds; that’s about 3 decimal digits every 5 iterations. Archie used it 4 times to go from hexagons to enneacontahexagons for an accuracy of about 3 decimal places. If he had bothered to repeat the process, say, ten more times, he would have known the first 9 decimal digits. Definitely not useful, but potentially brag-worthy.

Modern algorithms put those old approximations to shame instantly. Archimedes’ technique converges linearly to the true value of π (you gain about the same number of digits every time you use the algorithm). Things didn’t really start to pick up until we invented quadratically converging algorithms, which double the number of known digits with each iteration. That is: if you know ten, then after the next iteration you’ll know twenty. The fastest algorithms today converge nonically (the accurate decimal expansion gets nine times longer with each step).

The definition of π, the ratio of the circumference to the diameter of a circle, allows us to measure it directly, but inaccurately, or calculate it precisely, but pointlessly. The more abstract properties of π, like going on forever without repeating (which it does) or containing every possible pattern (which it might), require more than brute force discovery of digits. These more abstract properties are based on the definition of π, not its value, and can typically be proven or disproven without knowing even a single digit. Math is useful in the physical world, but it doesn’t “live here”. π has physical significance, but we use its mathematical properties to learn about it.

Answer Gravy: Ancient people were very clever and when they lived long enough they even got to prove it. This gravy is the math behind Archimedes’ algorithm. This isn’t exactly the way he wrote it. Ancient Greek mathematicians suffered from the demonstrably false belief that a minimum of words is the secret to a maximum of understanding. So, even translated, their proofs still read like Greek.

Mr. Medes’ method was this. If I_n is the perimeter of the inscribed polygon and C_n is the perimeter of the outer n-gon, then:

$C_{2n}=\frac{2C_nI_n}{C_n+I_n}\quad\quad I_{2n}=\sqrt{I_n C_{2n}}$

You could rigorously prove that as you increase the number of sides the perimeters will get closer to π (the circumference of the circle) using lots of equations or something, or you can just draw a picture and say “look… they clearly do”.

A circle (dashed line) with its inscribed and circumscribed n-gons (blue) and 2n-gons (red). The length of each segment is the total perimeter divided by the number of segments (hence all the dividing by n’s).

If you stick six triangles together, you get a hexagon and with a little trigonometry you find that if your circle has a diameter of 1, then the inscribed hexagon’s perimeter is I₆ = 3 and the circumscribed hexagon’s perimeter is C₆ = 2√3 ≈ 3.46.

To find the perimeters for dodecagons, plug C₆ and I₆ into the iterative equations:

$C_{12}=\frac{2(3.46)(3)}{3.46+3}\approx3.215$ $I_{12}=\sqrt{(3)(3.215)}\approx3.106$

These perimeters are both closer to π than those before the iteration and since $I_n<\pi<C_n$ for all n, this gives us an ever-diminishing range where π can be found. Here’s why it works:

In/circum-scribing n-gons on a circle produces some useful symmetries. In particular, it allows us to draw some triangles and rapidly figure out their angles.

One of the sides from an inscribed n-gon and a corner from a circumscribed n-gon. The lines inside are from the new 2n-gons. The red shaded triangles are similar to each other (have the same angles) and the blue outlined triangles are similar.

A full circle is 360 degrees, so each side of an n-gon spans 360/n degrees. In this case, a is half of one of those angles, so a=180/n.

Both b’s are complimentary to a (they sum to 90), since the sum of angles in a triangle is 180 and the third angle is 90 (a symmetry we get from the fact that radial lines always hit a circle at a right angle). So, b = 90-180/n.

c and b are complimentary, so c = a = 180/n.

c+d = 180, so d = 180-c = 180-180/n.

The sum of angles in a triangle is 180, so d+e+e = 180 and e = 90-d/2 = 90/n.

Finally, b+e+f = 90, so f = 90-b-e = 90/n.

Since f=e, the two red triangles have the same angles: they’re “similar triangles“. Similarly, since c=a the two blue triangles have the same angles and are also similar. When two triangles are similar, the ratios of their sides are the same.

The lengths involved.

Using the similarities on the blue triangles we can say:

$\begin{array}{rcl} \frac{\left(\frac{C_n}{2n}\right)}{\left(\frac{I_n}{2n}\right)}&=&\frac{\left(\frac{C_n}{2n}-\frac{C_{2n}}{4n}\right)}{\left(\frac{C_{2n}}{4n}\right)} \\[4mm] \frac{C_n}{I_n}&=&\frac{2C_n-C_{2n}}{C_{2n}} \\[2mm] \frac{C_n}{I_n}&=&\frac{2C_n}{C_{2n}}-1 \\[2mm] \frac{C_n}{I_n}+1&=&\frac{2C_n}{C_{2n}} \\[2mm] C_n+I_n&=&\frac{2C_nI_n}{C_{2n}} \\[2mm] C_{2n}\left(C_n+I_n\right)&=&2C_nI_n \\[2mm] C_{2n}&=&\frac{2C_nI_n}{C_n+I_n} \\[2mm] \end{array}$

and of course, using the red triangles:

$\begin{array}{rcl} \frac{\left(\frac{I_{2n}}{2n}\right)}{\left(\frac{C_{2n}}{4n}\right)}&=&\frac{\left(\frac{I_n}{n}\right)}{\left(\frac{I_{2n}}{2n}\right)} \\[4mm] \frac{I_{2n}}{C_{2n}}&=&\frac{I_n}{I_{2n}} \\[2mm] \left(I_{2n}\right)^2&=&I_nC_{2n} \\[2mm] I_{2n}&=&\sqrt{I_nC_{2n}} \\[2mm] \end{array}$

So, starting with a little geometry and the definition of π we can construct a bootstrapping method for approximating it better the longer we bother to work at it.

Multiplication and long division can be done by hand pretty easily. The hardest part of this iterative algorithm facing any ancient person is the square root. Also making the scratch paper. Fortunately, there are tricks for that too. For example, if you want to take the square root of S, just make a guess, x, then calculate $\frac{1}{2}\left(x+\frac{S}{x}\right)$ and what you get will be a number closer to $\sqrt{S}$ than your original guess, x. This method was known to the Babylonians and Archimedes (it is, in fact, “the Babylonian method”) and it converges quadratically, so it achieves whatever (reasonable) accuracy you’re hoping for almost instantly.

The point here is that you can, through the injudicious use of reason, time, and scratch paper alone, find π to as many digits as you would ever need.

You can read a little more about the Babylonian tablet here.

Posted in -- By the Physicist, Engineering, Geometry, Math | 10 Comments

Q: Given two points on the globe, how do you figure out the direction and distance to each other?

Posted on July 20, 2018 by The Physicist

Physicist: The very short answer is: use the spherical law of cosines so you can do trigonometry on a sphere.

This is a seriously old problem that needed to be solved before we became a routinely globe-trotting species. If you have the latitude and longitude of your location and a destination, you could just move east/west until you match the destination’s longitude then move north/south until you match the latitude. But that’s a big waste of time, as the so-intuitively-obvious-it-barely-deserves-a-name “triangle inequality” will tell you.

The “triangle inequality” says that the sum of any two sides of a triangle are longer than any one side. So if you’re traveling from Nicaragua to Norway, don’t go via Nigeria.

As you may have heard, the shortest distance between two points is a straight line. For curved surfaces the closest you can get to a straight line is a “geodesic”, which is a straight line on small scales, but it you step back may be going all over the place. If you wrap a ribbon around a gift (or any manner of festive package) and manage to keep it flat, you’ve found a geodesic, because if the path of the ribbon changes direction, the ribbon kinks. On a sphere like Earth, where you’re stuck moving along the surface (instead of drilling straight through like some kind of compulsive, fire-proof mole), the geodesics are “great circles”. If you walk in a straight line, you’re walking on a great circle.

A great circle is the path you’ll follow if you walk in a straight line on a sphere. Smaller circles result from not-straight-lines (continuously turning a little to the side).

Doing geometry on a sphere is more difficult than geometry on a flat plane, but not by a hell of a lot. Geometry, despite what some pudunk Greek philosophers may say, is basically just playing with triangles. A nice, universal rule for any triangle is the Law of Cosines which relates the lengths of the three sides, a, b, and c, with the angle opposite one of those sides, C: $c^2=a^2+b^2-2ab\cos(C)$ .

Left: A triangle made from great arcs. Right: A triangle made from straight lines.

Slap that triangle on the side of a sphere and that law becomes the Spherical Law of Cosines:

$\cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C)$

Here the meaning of a, b, and c has changed a little. Lengths on a sphere can be described by angles (drawn from the center to the surface). If you’re using radians (which you always should), those angles are $\frac{\textrm{the overland distance}}{\textrm{Earth's radius}}$ . This is generally easier to use than the actual distance. For example, the angle from the north pole to the equator is 90° (obviously) while the physical distance is about 6,200 miles (different on every planet).

Lucky for us, positions on Earth are usually described in terms of angles (latitude and longitude) and not distances, so the spherical law of cosines is ready to go. Just put the corners at the north pole, where you’re at, and where you’re planning to go.

If you put the corners of the triangle at a pole, your location, and your destination, then you can read off the lengths of two sides (90-latitude) and the angle at the pole (the difference of the longitudes). From these there’s enough information to find the distance and bearing to the destination.

The law of cosines (either of them) relates four things: all three sides and one of the angles. If you have any three of those pieces of information you can solve for the forth. With the latitudes we have two sides and with the difference of the longitudes we got an angle.

First (because you always should) convert your angles from degrees to radians by multiplying by $\frac{\pi}{180}$ : $\theta_1=\frac{\pi}{180}(90-latitude1)$ , $\theta_2=\frac{\pi}{180}(90-latitude2)$ , and $\phi=\frac{\pi}{180}|longitude1-longitude2|$ .

$\cos\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)=\cos\left(\theta_1\right)\cos(\theta_2)+\sin\left(\theta_1\right)\sin(\theta_2)\cos(\phi)$

and therefore

$\textrm{distance}=(\textrm{Earth's radius})\arccos\left[\cos\left(\theta_1\right)\cos(\theta_2)+\sin\left(\theta_1\right)\sin(\theta_2)\cos(\phi)\right]$

Boom! There’s the distance. And with three sides in hand (the two given by the latitudes and the distance from, like, two seconds ago) you can find your “bearing”, the angle between north and your destination.

$\cos\left(\theta_2\right)=\cos\left(\theta_1\right)\cos\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)+\sin\left(\theta_1\right)\sin\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)\cos\left(\textrm{bearing}\right)$

and so

$\textrm{bearing}=\arccos\left[\frac{\cos\left(\theta_2\right)-\cos\left(\theta_1\right)\cos\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)}{\sin\left(\theta_1\right)\sin\left(\frac{\textrm{distance}}{\textrm{Earth's radius}}\right)}\right]$

For example, if you happen to be traveling from Nueva Guinea, Nicaragua (11.6932° N, 84.4540° W) to Nesflaten, Norway (59.6466° N, 6.7997° E), the angles involved are $\theta_1=\frac{\pi}{180}(90-11.6932)\approx1.367$ , $\theta_2=\frac{\pi}{180}(90-59.6466)\approx0.530$ , and $\phi=\frac{\pi}{180}\left|6.7997-(-84.4540)\right|\approx1.593$ . So the distance is

$\textrm{distance}=(3959miles)\arccos\left[\cos\left(1.367\right)\cos(0.530)+\sin\left(1.367\right)\sin(0.530)\cos(1.593)\right]=(3959miles)(1.406)=5566miles$

and the bearing is

$\textrm{bearing}=\arccos\left[\frac{\cos\left(0.530\right)-\cos\left(1.367\right)\cos\left(\frac{5566}{3959}\right)}{\sin\left(1.367\right)\sin\left(\frac{5566}{3959}\right)}\right]=0.538rad=30.1^o$

If you want to walk in a straight line from downtown Nueva Guinea to uptown Nesflaten, you’d face due north, turn about 30 degrees to the right, and walk in a straight line for about two and a half months, while ignoring the Atlantic Ocean to the best of your ability.

So how do you calculate distance and bearing? A small bucket of math. Today if you want to calculate sines and cosines you break out a computer. So you may be wondering how they did this math back in the days of sailing ships (without GPS). They didn’t. Calculating was done once, then written down, then looked up many times. Once upon a time books were useful!

A very boring book from the 17th century wherein you can look up the values of trig functions.

The people who actually did the calculating were “computers”; pitiable folk who sat in dark rooms and slowly went mad and rarely got to sail around the world.

Posted in -- By the Physicist, Geometry, Math | 9 Comments

Q: Is it possible to eat all of the ice cream in a bowl?

Posted on July 2, 2018 by The Physicist

Physicist: If you’ve ever sat next to someone as they rang an almost-empty ice cream bowl like church bells on Sunday, then you’ve probably asked yourself some variation of this question.

Still plenty left.

Clearly, the issue is that a spoon and a bowl aren’t osculating curves. The radius of a spoon’s curvature is typically less than an inch while a bowl’s is several inches. With different curvatures, when you drag a spoon across the bottom of an ice-cream-laden bowl, they only contact each other at a tiny point and you can only remove ice cream along a thin strip (Matching the curvatures is why you instinctively start using the spoon sideways when the ice cream is low). So if you wanna get your bowl perfectly clean, you gotta figure out how wide that strip is.

Around the point of contact there’s a gap between the spoon and bowl that gets bigger the farther away you get. But so long as the ice cream molecules are bigger than that gap, they’ll be caught. Water, at about a quarter of a nanometer across, is the smallest molecule in ice cream’s molecular menagerie.

To figure out the width of the strip (red bar) removed by the pass of a spoon, you have to find how far you can get from the point of contact before the gap is big enough for the smallest molecules to pass through.

The bottom of a circle with a radius R can be closely approximated by a parabola of the form $y=\frac{1}{2R}x^2$ (There’s nothing too special about parabolas; every curve that doesn’t have sharp corners can be closely approximated by circles and vice versa, it’s just that parabola math is easy). Spoons have a radius of around 1 cm. Bowls have a radius of around 7 cm. The distance from the center (the point of contact) to the edge of the strip, x, such that water molecules won’t be able to slip through the gap between the bowl and the passing spoon is given by $\frac{1}{2(0.01m)}x^2-\frac{1}{2(0.07m)}x^2=0.25\times10^{-9}m$ . Solve for x and you get $x=2.4\times10^{-6}m$ , so the strip should be about 5 micrometers across; on the order of a tenth of a hair’s width.

The wide ice-cream-free swaths you see in practice aren’t regions where all of the ice cream has been removed, but regions where it’s been left thin enough to see though. So, if you really wanted to scrape a bowl clean of every molecule of ice cream, you’d need to carefully “scan” one strip after another, about four million and change times. Just to make sure you don’t miss any (else you and your IC OCD would be forced to start over), it couldn’t hurt for those strips to overlap. Call it an even ten million passes. At, say, two passes per second (the approximate speed of a kid charging headlong into a brain freeze), it would take you almost two months to scour your bowl clean. About a week into that, you’ll get the overwhelming urge to ask for seconds. Or at least do something else.

So far, this is all a bit idealized. The Platonic perfection of parabolas doesn’t apply to actual spoons and bowls. If you zoom in close enough, ceramics are like moonscapes with plenty of room for ice cream to hide and the tip of a spoon looks more like a stainless steel mountain range. Truly, a rocky road.

The surface of a ceramic with the (highly ideal) 5 micrometer wide ice-cream-molecule-stripping path of a spoon.

As undeniably clever as the approach above is, that “10,000,000 passes with a spoon” estimate is built on unrealistic premises. Sadly, you can’t eat all the ice cream in a conventional bowl using compulsive spooning alone.

But that doesn’t mean it’s impossible eat all of the ice cream, you just have to stretch the rules a little. For example, you could eat as much as you would like, then put the bowl into a kiln. By and large, organic molecules (sugar, fat, cellulose, etc.) burn at temperatures below 500°F and turn into new compounds, and a good kiln heats things up to 1700°F. A ceramic bowl would survive the heat intact, but the chemicals that make ice cream ice cream (as opposed to ash) wouldn’t.

No ice cream may escape.

So if you define “eating all the ice cream in the bowl” as “there was ice cream, I ate ice cream, now it’s all gone”, a kiln is a good way to do it. But if you think destroying the evidence is somehow cheating, there is one more, perhaps not as delicious, alternative guaranteed to work.

Eat the bowl.

Willy Wonka demonstrating the simplest solution for consuming every atom of ice cream (or whatever else).

The empty ice cream bowl picture is from here.

The extreme close-up of a ceramic is from here.

The kiln picture is from here.

The Willy Wonka picture is from Willy Freaking Wonka.

Posted in -- By the Physicist, Geometry, Philosophical | 11 Comments

Ask a Mathematician / Ask a Physicist

Q: What is the “monogamy of entanglement”?

Q: Could dark matter actually be the “gravitational shadow” of parallel universes?

Burning Man’s Mathematical Underbelly

Q: How was the number π first discovered? How did we first figure out it was 3.14…?

Q: Given two points on the globe, how do you figure out the direction and distance to each other?

Q: Is it possible to eat all of the ice cream in a bowl?

Send your questions about math, physics, or anything else you can think of to:

Subscribe via Email

Search the Archives

Categories

Archives

Recent