Ask a Mathematician / Ask a Physicist

Physicist: The Copenhagen interpretation requires that new laws be created that, in addition to being impossible, are completely unnecessary, physically unfeasible, and utterly unjustifiable.  The basic laws of quantum mechanics, when applied at all scales, give you the Many Worlds interpretation.  No fancy rules, no awkward questions.  Even better, what seems to be wave function collapse in Copenhagen is actually described by the Many Worlds approach.  So why choose the Copenhagen interpretation over Many Worlds?  No damn reason at all.

Many Worlds vs. Copenhagen. On the one hand there are different versions of you, and on the other you've got vaguely defined mental powers.

If you’re already familiar with the basic ideas behind the measurement problem, and the divide between Copenhagen and MW, feel free to skip down to the word “catawampus“.

Bell’s theorem demonstrated that either information travels faster than light (Bohm) or particles exist in many states simultaneously (everybody else).  There is a lot wrong with Bohm’s theories, not the least of which is that it doesn’t have a relativistic formulation (which may not sound too bad, but that’s really damning in physics circles).

The best example is the double slit experiment: shine coherent light on two slits and look at the pattern that’s projected onto a screen.  You get a nice interference pattern of dark and light bands on the screen, which is fine since light is a wave (don’t stress about wave/particleness here).  What’s messed up is that even when the light intensity is turned way down to just one photon at a time, the photon still tends to land where the bright bands were, and almost never lands where the dark bands were.

You have to repeat the single-photon double-slit experiment a lot to see the pattern, but there it is. In order to get these interference fringes from two slits the photon must interfere with itself. It's going through both.

Alright, so everybody has come to accept that very small things have no problem being in several states simultaneously (if you don’t buy it, then just take it as read).  But here’s the weirdness.  It turns out that particles only exhibit the super-position properties when “you” can’t tell the difference between the various states.  As soon as “you” can single one out, then suddenly the super-positionness goes away.  I’m putting quotes (“”) around “you”, because “you” could be a person, or a computer, or even another particle.  Just a weakness of the language.

This is the measurement problem.  Things can be in several states at the same time, but only if nothing observes* them.  The moment they’re observed* they are found to be in only one state, and they continue on their merry way in only that one state.  The most straight forward (brute force) example is covering one slit and noting that the interference bands disappear.  By covering one slit you’re “observing*” that the photon is going through the other.  Most examples are more complex and subtle.

(* this is another weakness of the language.  “Observe” would seem to imply a hierarchy; “this observes that”.  A better term might be “interact with”.)

Here’s where the split comes up.  Copenhagenists will say that something, usually size, or complexity, or random collapse, or, worst of all, consciousness, causes “wave function collapse” (all but one state disappears).

Many Worlds adherents will say that wave function collapse never happens, and that the trick is realizing that both the particles involved and the observer* are in multiple states.  After the observation* the multiple states of the particle are now entangled with the multiple states of the observer*.  In the double-slit test you’d have the two states: “photon goes right and observer sees it go right” and “photon goes left and observer sees it go left”.  Both states persist, and there’s no collapse.

Catawampus: You’ll often hear that there’s no experiment that can be done to prove which approach is the correct one.  I’m of the opinion that the experiments have already been done, but that most people (myself included) don’t like the results.  However, among people who have stopped to consider the options (and there aren’t many good reasons to do so), most of us have decided to accept the results and move on.

The big advantage behind the Copenhagen interpretation is that it makes people (like you!) important, and different from particles.  <sarcasm>Sure, they may be in multiple states, but I’m definitely in exactly one state.  Unlike particles, people can tell the difference.</sarcasm>

It’s creepy to think that there are different versions of yourself “out there” doing “stuff”, but it’s awesome to assume that you’re special and that your mind (not brain) has some kind of power over reality.

There is a version of the Copenhagen interpretation of quantum mechanics where consciousness (usually human, sometimes God, sometimes Gaea, …) plays a key role.  I feel pretty comfortable dismissing it out of hand.  There’s a post here that talks about it a little.

Time and again, we’ve managed to show that larger and larger objects can be in multiple states, using the double slit experiment or variations of it.  At last check, the double slit experiment was successfully preformed on C₆₀F₄₈, which has fully 108 atoms, or 2,424 protons, neutrons, and electrons.  The entire molecule (actually, thousands of them) actually interfered with itself, demonstrating the ability to be in multiple states.

Which raises the question: what’s the damn problem?  Everything that can be tested has demonstrated quantum superposition, so why not just extend that to “everything obeys the same quantum mechanical laws, including superposition.”?  Why not indeed?

One may be tempted to say “the physics at small scales is just different!”.  Fair enough.  However, there are no physical laws that work differently on different scales.  For example, at very small scales water acts like honey, and to swim you need to use things like flagella.  At the other end of the scale (our scale) water behaves… like water, and things like fins and flippers suddenly work really well, but flagella don’t.  However, the same physical laws (specifically, the Navier-Stokes equation) govern everything.

More generally, all laws apply at all scales, it’s just a question of degree.  Relativity works at all velocities, but you don’t notice the weird effects until you’re moving really fast.  What we call “Newton’s laws” are just an approximation that work at low speeds.

If the Copenhagen “size argument” (that larger objects somehow have different laws) holds up, it’ll be the first of its kind.

So how can the many worlds hypothesis hold up?  Either we’re in multiple states or we’re not, and (most) people don’t feel like they’re in more than one state.

In very much the same sense that relativity includes Newtonian dynamics as a special case, the Many World hypothesis actually contains Copenhagenism.

Normally in quantum mechanics, when you’re trying to predict the behavior of a system, you just let all the components evolve in time according to the Schrödinger equation.  If you follow a particular state or object, then you’ll find that it experiences wave function collapse all over the place.

That is to say: If you require (artificially) that some particular thing must remain in one state (or small set of states) by disregarding its other states, then that object will (seem) to see wave function collapse.

I should repeat that, because it bears repeating:

According to the Many Worlds approach, the individual states of an object witness wave function collapse all the time, but taken as a whole, there is no collapse.

Here’s an simplified example with very little physical basis, but that hopefully gets the point across.

In what follows the are collision points.  Either the particles pass each other, or bounce off each other and change direction.  They can’t both go down the same path.  The are splitters.  When a particle hits this it has a 50% chance of passing, and 50% chance of reflecting.

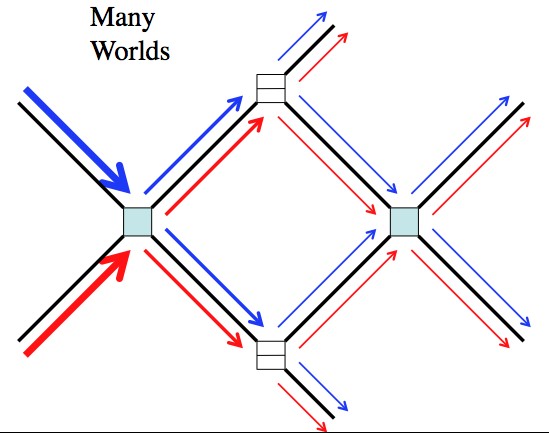
To calculate the probabilities of how the two quantum particles will come out of the machine you have to sum over ever possible path. You have to take into account, not only every "choice", but every interaction.

This map shows how two particle move through some machine.  Either they bounce off each other at the first and you have blue-up/red-down, or they pass each other and you have blue-down/red-up.  These two states then go on to the splitters and so on.  There is no collapse, and every possibility (every path, every interaction) is included (like the double slit).

But what if you were the to track the blue particle?  Put your foot down and insisted that it remain in just one state and take just one path through the machine?  Even more profound, what is the effect on the red particle (from the new one-path-point-of-view of the blue particle)?

Easy enough, pick one of the blue paths (worlds) above.

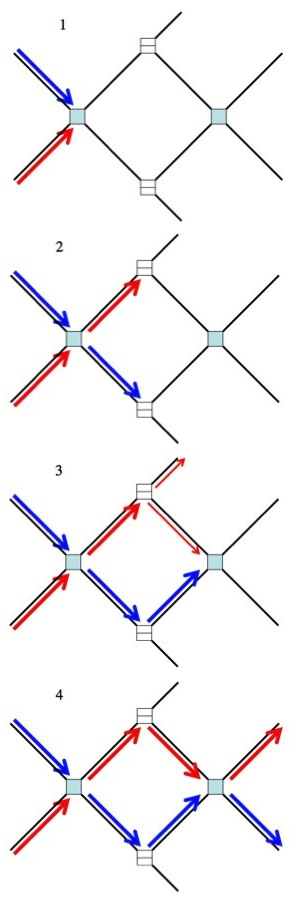
1) The particles start. 2) In this world they pass each other. They didn't have to, they just happened too. 3) Since we're insisting the blue particle stays on one path, it must pick a path: reflect. The red particle, however, is free to take multiple paths, and does. 4) In this world the blue particle bounces off the red particle at the second box. But this interaction means that the blue particle now knows where the red particle is. Collapse!

This story is just one of the stories encompassed in the Many Worlds picture.

Here’s a slightly different one.  What would happen if the blue particle went through the splitter instead of reflecting?

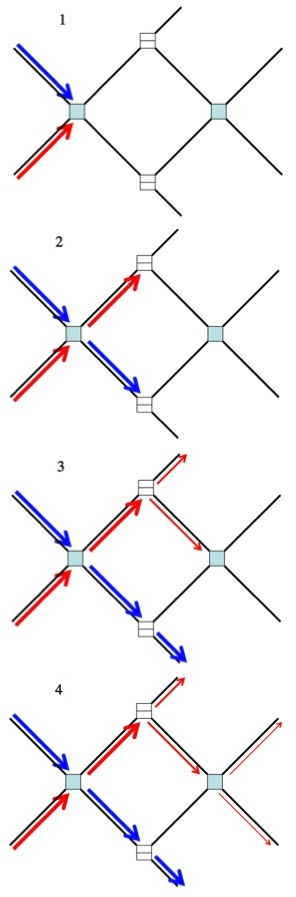
1&2) Same as last time. 3) Since we insisted that the blue particle must be in one state, it must either reflect or pass. In this case it passes. The red takes both available paths. 4) The blue particle can't interact with the red, so this time the red particle is free to take even more paths simultaneously (as far as this version of the blue particle is concerned).

So the big point is that the Copenhagen wave function collapse is strictly an illusion created by restricting your attention to a particular state of one object.  So why is our attention stuck on just one state?  We’re not special, just victims of conservation laws.

Looking down on the double slit experiment from outside you can ask questions like “what is the probability that the photon will go through each slot?”.  You have no “givens” to affect your probabilities so you say “50/50”, and you’re right.  The photon goes through both, but since there’s only one photon (conserved number of photons), it does it in a particular (some what obvious) way: it combines the states “left/not right” and “not left/right”.

Now say you’re presented with two doors.  You also can’t be in the state “right and left”.  Now when you go through one door, because you’re interacting with yourself, you have givens that affect the probabilities.  Ask yourself, “What is the probability that I went through the left door, given that I just went through the right door?”  Zero, baby!

The version of you that when through the left door will be able to make a very similar calculation.

Finally (without going into too much detail), the Copenhagen interpretation also violates a number of very straight forward physical laws.  Conservation of information (supported by everything else, including logic), time reversibility (again, everything else), and information flowing backward through time (spacelike information exchange or “spooky action at a distance”) are only the most direct and grievous examples.