Q: Will we ever overcome the Heisenberg uncertainty principle?

Posted on August 1, 2010 by The Physicist

Physicist: Nopers!

The Heisenberg uncertainty principle, while normally presented in physics circles, is actually a mathematical absolute.  So overcoming the uncertainty principle is exactly as hard as overcoming that whole “1+1=2” thing.

The uncertainty principle (the “position/momentum uncertainty principle”) is generally presented like this: you have some particle floating along and you’d like to know its position and its momentum (velocity, whatever) so you bounce a photon off of it (“Bounce a photon off of it” is just another way of saying “try to see it”).  A general rule of thumb for light (waves in general really) is high frequency waves propagate in straight lines, and low frequency waves spread out.  That’s why sunlight (high frequency) seems to go in a perfectly straight line, but radio waves can spread out around corners.  For example, you can still pick up a radio station even when you can’t see it directly.

So, if you want to see where something is with precision you’ll need to use a high frequency photon.  After all, how can you trust the results from a wandering, low frequency photon?  But, if you use a precise, high-frequency, and thus, high-energy photon, you’ll end up smacking the hell out of the particle you’re trying to measure.  So you’ll know where it is pretty exactly, but it’ll go flying off with some unknown amount of momentum.  Any method you can come up with to measure the momentum will require you to use low-frequency, low-energy, gentle photons.  But then you won’t be able to figure out the particle’s position very well.

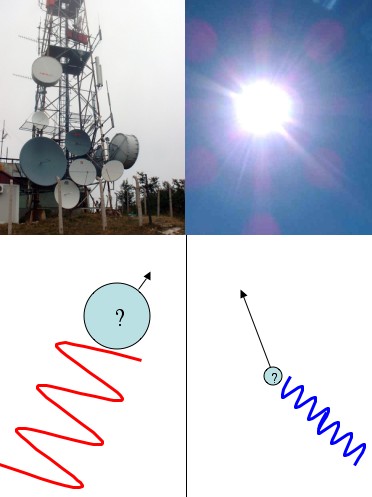
Low frequency photons (like radio waves) don't tell you much about where a particle is, but they doesn't knock it around much either (so you can measure its momentum better). High frequency photons (like sunlight) are terrible at measuring momentum, but can tell you position well.

So far this seems more like an engineering problem than a problem with the universe.  Maybe we could arrange things so that the high frequency photon hit softer or something?  There was a lot of back and forth for a long time (still is in some circles) about overcoming the uncertainty principle, but in the end it can never be violated.

Rather than being something that’s merely very challenging like, “you can’t break the sound barrier”, “what goes up must come down”, and “you can’t be the world’s best kick-boxer and be the world’s most handsome physicist”, the uncertainty principle is a mathematical absolute.  So, unless the basic assumptions of physics are completely wrong (and they’ve held up to some serious scrutiny), the uncertainty principle is in the company of things like “you can’t go faster than light”, “energy and mass are conserved”, and “modern mathematicians don’t have beards” (has anyone else noticed this?).  What follows is answer gravy.

Answer gravy: This gravy has some lumps.  If you know what a “Fourier transform” is, and are at least a little comfortable with them, then this could be interesting to you.

The square of a quantum wave function is the probability of finding it in a particular state.  For example, the “position wave function” can tell you the probability of finding a particle at any position. To get the probability from the wave function, all you have to do is square the wave function.

If you’ve got the quantum wave function f(x) for the position of a particle, then you can find the the momentum wave function, g(p), by taking the Fourier transform of f.  That is, g=\hat{f}.  Now, you can define the uncertainty as the standard deviation of the probability function, which is a really good way to go about it.

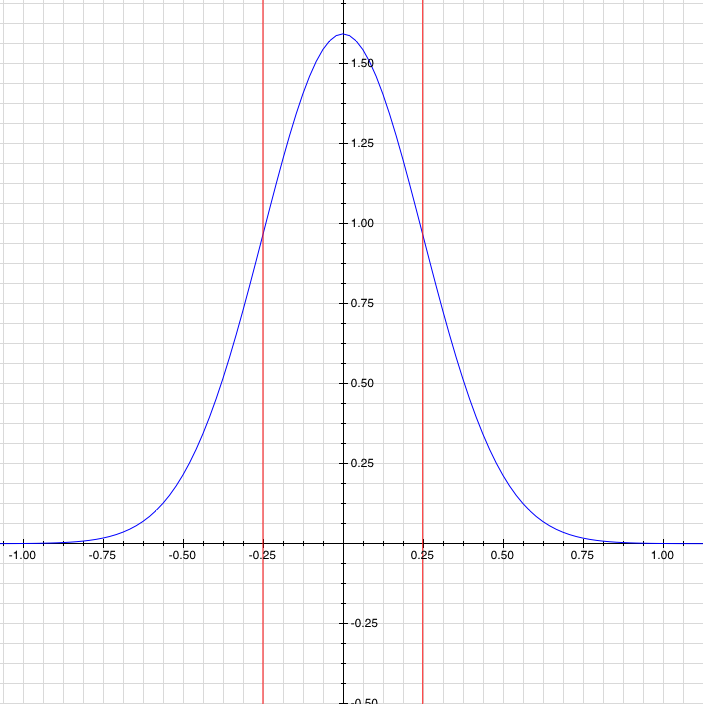
A probability function (blue), with its uncertainty or standard deviation (red). Like you'd expect, the particle is most likely to be near zero, but it's not certain to be near zero.

The uncertainty principle now just boils down to the statement that the product of the uncertainties of the square of a function, f, and the square of its Fourier transform, \hat{f}, is always greater than some constant.  In what follows you’ll find some useful stuff such as Plancherel’s theorem and Cauchy-Schwartz.

\begin{array}{ll}\sigma_x\sigma_p=\sigma_{|f|^2}\sigma_{|\hat{f}|^2}\\=\sqrt{Var(|f|^2)}\sqrt{Var(|\hat{f}|^2)}\\=\left(\int x^2|f|^2\,dx\right)^{\frac{1}{2}}\left(\int\xi^2|\hat{f}|^2\,d\xi\right)^{\frac{1}{2}}\\=\left(\int |xf|^2\,dx\right)^{\frac{1}{2}}\left(\int|\xi\hat{f}|^2\,d\xi\right)^{\frac{1}{2}}\\=\frac{1}{2\pi}\left(\int |xf|^2\,dx\right)^{\frac{1}{2}}\,\left(\int|\widehat{f^\prime}|^2\,d\xi\right)^{\frac{1}{2}}&(\widehat{f^\prime}=2\pi i\xi\hat{f})\\=\frac{1}{2\pi}\left(\int |xf|^2\,dx\right)^{\frac{1}{2}}\,\left(\int|f^\prime|^2\,d\xi\right)^{\frac{1}{2}}&(\textrm{Plancherel})\\ \ge\frac{1}{2\pi}\int|xf f^\prime|\,dx&(\textrm{Cauchy-Schwartz})\\=\frac{1}{2 \pi} \int |x| \, |f| \, |f^\prime| \, dx \\\ge \frac{1}{2 \pi} \left| \int x |f| f^\prime \, dx \right| \\= \frac{1}{2 \pi} \left| \int (x) (\frac{1}{2}|f|^2)^\prime \, dx \right|&(\frac{1}{2}|f|^2)^\prime=|f| f^\prime\\= \frac{1}{4 \pi} \left| \int |f|^2 \, dx \right|&(\textrm{integration by parts})\\=\frac{1}{4 \pi}&(\textrm{the total probability is always 1})\end{array}

So, there’s the Heisenberg uncertainty principle: \sigma_{|f|^2} \sigma_{|\hat{f}|^2} \ge \frac{1}{4 \pi}.  A physicist would recognize this as \Delta x \Delta p \ge \frac{\hbar}{2}.  The difference comes about because the Fourier transform that takes you from the position wave function to the momentum wave function involves an h, and \hbar = \frac{h}{2\pi}.  (For the physicists out there who were wondering what happened to their precious h’s)

Posted in -- By the Physicist, Equations, Math, Physics, Probability, Quantum Theory | 24 Comments

Q: If gravity is the reaction matter has on space, in that it warps space, why do physicist’s look for a gravity particle? Wouldn’t gravity be just a bi-product of what matter does to space?

Posted on July 31, 2010 by The Physicist

Physicist: Isn’t that weird?

The name “quantum mechanics” comes from the fact that, at its most base, quantum mechanics requires all particles and energies to come in discrete (one might say “quantized”) packets.  At some point a bunch of physicists starting asking awkward questions like; the matter is quantized, the energy is exchanged in quantized packets, so why do we assume the force is smooth and continuous?

Compounding this awkward line of questioning was the fact that photons were already known to carry electromagnetic force.  Literally, photons are little oscillating bits of electric and magnetic fields, which is exactly what the electric and magnetic forces are.  So the next obvious question was “do the other forces have ‘force carriers‘?”

You’re damn right they do.  Photons for electromagnetism, W and Z bosons for the nuclear weak force, and gluons for the nuclear strong force.  There’s every force but gravity!  Each of the carriers were predicted by the (then new) study of “quantum field theory”, and have since been observed.  The theory itself is gorgeous and works beautifully.  In fact, it barely makes sense to think of anything in the universe (including space) as not being quantized.

So, some physicists are looking for evidence of the existence of gravitons (the gravity particle), because it would really tie things together nicely.  There are a couple drawbacks however…  In order for something to be detected it has to do something.  Gravity is a really, really weak force, and a graviton is the smallest amount of that force that can exist.  Most physicists have already given up any hope of detecting the graviton directly, and instead are looking at extremely indirect methods.  The drawback there is that the graviton (if it exists, and if our theories hold up) is a very strange particle, and is described using amazingly nasty math (even more nasty than the normally nasty math of quantum field theory).  So it’s difficult to even figure out what those indirect methods should be.

To actually answer the question: some physicists are looking for the graviton because it “fits”.

Posted in -- By the Physicist, Particle Physics, Physics, Quantum Theory | 12 Comments

Q: Is it possible to beat the laws of physics?

Posted on July 26, 2010 by The Physicist

Physicist: No…
But to be fair, when a physical law is beaten it stops being a law.

Posted in -- By the Physicist, Paranoia, Philosophical, Skepticism | 8 Comments

Q: What’s the chance of getting a run of K or more successes (heads) in a row in N Bernoulli trials (coin flips)? Why use approximations when the exact answer is known?

Posted on July 24, 2010 by The Physicist

The original question was: Recently I’ve come across a task to calculate the probability that a run of at least K successes occurs in a series of N (K≤N) Bernoulli trials (weighted coin flips), i.e. “what’s the probability that in 50 coin tosses one has a streak of 20 heads?”. This turned out to be a very difficult question and the best answer I found was a couple of approximations.

So my question to a mathematician is: “Why is this task so difficult compared e.g. to finding the probability of getting 20 heads in 50 coin tosses solved easily using binomial formula? How is this task in fact solved – is there an exact analytic solution? What are the main (preferably simplest) approximations and why are they used instead of an analytic solution?”

Physicist: What follows was not obvious. It was the result of several false starts. It’s impressive in the same sense that a dude with seriously bruised legs, who can find anything in his house with the lights off, is also impressive. If you’re looking for the discussion of the gross philosophy, and not the detailed math, skip down to where you find the word “Jabberwocky” in bold. If you want specific answers for fixed, small numbers of coins, or you want sample computer code for calculating the answer, go to the bottom of the article.

The short answer: the probability, S, of getting K or more heads in a row in N independent attempts (where p is the probability of heads and q=1-p is the probability of tails) is:

S(N,K) = p^K\sum_{T=0}^\infty {N-(T+1)K\choose T}(-qp^K)^T-\sum_{T=1}^\infty {N-TK\choose T}(-qp^K)^T

Note that here {A\choose B} is the choose function (also called the binomial coefficients) and we are applying a non-standard convention that {A\choose B}= 0 for A < B which makes the seemingly infinite sums always have only a finite number of terms. In fact, for N and K fixed, the answer is a polynomial with respect to the variable p.

Originally this was a pure math question that didn’t seem interesting to a larger audience, but we both worked for long enough on it that it seems a shame to let it go to waste. Plus, it gives me a chance to show how sloppy (physics type) mathematics is better than exact (math type) mathematics.

Define {Xi}j as the list of results of the first j trials. e.g., if j=4, then {Xi}j might be “{Xi}4=HTHH” or “{Xi}4=TTTH” or something like that, where H=heads and T=tails. In the second case, X1=T, X2=T, X3=T, and X4=H.

Define “Ej” as the event that there is a run of K successes (heads) in the first j trials. The question boils down to finding P(EN).

Define “Aj” as the event that the last K terms of {Xi}j are T followed by K-1 H’s ({Xi}j = X1X2X3X4…THHH…HHH). That is to say, if the next coin (Xj+1) is heads, then you’ve got a run of K.

Finally, define p = P(H) and q = P(T) = 1-p. Keep in mind that a “bar” over an event means “not”. So “\overline{H}=T” reads “not heads equals tails”

The probability of an event is the sum of the probabilities of the different (disjoint) ways that event can happen. So:

\begin{array}{ll}&P(E_{j+1})\\i)&=P(E_{j+1}\cap E_j\cap A_j)+P(E_{j+1}\cap E_j\cap \overline{A_j})+P(E_{j+1}\cap \overline{E_j}\cap A_j)+P(E_{j+1}\cap \overline{E_j}\cap \overline{A_j})\\ii)&=\left[P(E_{j+1}\cap E_j\cap A_j)+P(E_{j+1}\cap E_j\cap \overline{A_j})\right]+P(E_{j+1}\cap \overline{E_j}\cap A_j)+P(E_{j+1}\cap \overline{E_j}\cap \overline{A_j})\\iii)&=\left[P(E_{j+1}\cap E_j)\right]+P(E_{j+1}\cap \overline{E_j}\cap A_j)+P(E_{j+1}\cap \overline{E_j}\cap \overline{A_j})\\iv)&=P(E_j)+P(E_{j+1}\cap \overline{E_j}\cap A_j)+P(E_{j+1}\cap \overline{E_j}\cap \overline{A_j})\\v)&=P(E_j)+P(E_{j+1}\cap \overline{E_j}\cap A_j)+0\\vi)&=P(E_j)+P(E_{j+1}|\overline{E_j}\cap A_j)P(\overline{E_j}\cap A_j)\\vii)&=P(E_j)+pP(\overline{E_j}\cap A_j)\\viii)&=P(E_j)+pP(\overline{E_j}| A_j)P(A_j)\\ix)&=P(E_j)+pP(\overline{E_j}| A_j)qp^{K-1}\\x)&=P(E_j)+qp^KP(\overline{E_{j-k}})\\xi)&=P(E_j)+qp^K\left[1-P(E_{j-k})\right]\\xii)&=P(E_j)+qp^K-qp^KP(E_{j-k})\end{array}

iv) comes from the fact that E_j \subset E_{j+1}. If you have a run of K heads in the first j trials, of course you’ll have a run in the first j+1 trials. v) The zero comes from the fact that if the first j terms don’t have a run of K heads and the last K-1 terms are not all heads, then it doesn’t matter what the j+1 coin is, you can’t have a run of K heads (you can’t have the event Ej+1 and not Ej and not Aj). vii) is because if there is no run of K heads in the first j trials, but the last K-1 of those j trials are all heads, then the chance that there will be a run of K in the first j+1 trials is just the chance that the next trial comes up heads, which is p. ix) the chance of the last K trials being a tails followed by K-1 heads is qpK-1. x) If the last K (of j) trials are a tails followed by K-1 heads, then whether a run of K heads does or doesn’t happen is determined in the first j-K trials.
The other steps are all probability identities (specifically P(C)=P(C\cap D)+P(C\cap \overline{D}), \, P(\overline{C})=1-P(C), and Bayes’ theorem: P(C\cap D)=P(C|D)P(D)).

Rewriting this with some N’s instead of j’s, we’ve got a kick-ass recursion: P(E_N)=P(E_{N-1})+qp^K-qp^KP(E_{N-K-1})

And just to clean up the notation, define S(N,K) as the probability of getting a string of K heads in N trials (up until now this was P(EN)).

S(N,K)=S(N-1,K)+qpK-qpKS(N-K-1,K). We can quickly figure out two special cases: S(K,K) = pK, and S(l,K) = 0 when l<K, and that there’s no way of getting K heads without flipping at least K coins. Now check it:

\begin{array}{ll}&S(N,K)\\i)&=S(N-1,K)+qp^K-qp^KS(N-K-1,K)\\ii)&=\left[S(N-2,K)+qp^K-qp^KS(N-K-2,K)\right]+qp^K-qp^KS(N-K-1,K)\\iii)&=S(N-2,K)+2qp^K-qp^K\left[ S(N-K-1,K)+S(N-K-2,K)\right]\\iv)&=S(N-3,K)+3qp^K-qp^K\left[ S(N-K-1,K)+S(N-K-2,K)+S(N-K-3,K)\right]\\v)&=S(N-(N-K),K)+(N-K)qp^K-qp^K\left[ S(N-K-1,K)+\cdots+S(N-K-(N-K),K)\right]\\vi)&=S(K,K)+(N-K)qp^K-qp^K\left[ S(N-K-1,K)+\cdots+S(0,K)\right]\\vii)&=p^K+(N-K)qp^K-qp^K\sum_{r=0}^{N-K-1} S(r,K)\\viii)&=p^k+(N-K)qp^K-qp^K\sum_{r=K}^{N-K-1} S(r,K)\end{array}

ii) Plug the equation for S(N,K) in for S(N-1,K). iii-vi) is the same thing. vii) write the pattern as a sum. viii) the terms up to K-1 are all zero, so drop them.

Holy crap! A newer, even better recursion! It seems best to plug it back into itself!

\begin{array}{ll}i)&S(N,K)=p^K+(N-K)qp^K-qp^K\sum_{r=K}^{N-K-1} S(r,K)\\ii)&=p^K+(N-K)qp^K-qp^K\sum_{r=K}^{N-K-1} \left[p^k+(r-K)qp^K-qp^K\sum_{\ell=K}^{r-K-1} S(\ell,K)\right]\\iii)&=p^K+(N-K)qp^K-qp^K\sum_{r=K}^{N-K-1}p^k-qp^K\sum_{r=K}^{N-K-1}(r-K)qp^K+\left(qp^K\right)^2\sum_{r=K}^{N-K-1}\sum_{\ell=K}^{r-K-1} S(\ell,K)\\iv)&=p^K+(N-K)qp^K-qp^K\sum_{r=1}^{N-2K}p^k-\left(qp^K\right)^2\sum_{r=0}^{N-2K-1}r+\left(qp^K\right)^2\sum_{r=2K+1}^{N-K-1}\sum_{\ell=K}^{r-K-1} S(\ell,K)\\v)&=p^K+(N-K)qp^K-p^k(N-2K)qp^K-\left(qp^K\right)^2\frac{(N-2K)(N-2K-1)}{2}+\left(qp^K\right)^2\sum_{r=2K+1}^{N-K-1}\sum_{\ell=K}^{r-K-1} S(\ell,K)\\vi)&=p^K+{N-K\choose 1}qp^K-p^K{N-2K\choose 1}qp^K-{N-2K\choose 2}\left(qp^K\right)^2+\left(qp^K\right)^2\sum_{r=2K+1}^{N-K-1}\sum_{\ell=K}^{r-K-1} S(\ell,K)\end{array}

You can keep plugging the “newer recursion” back in again and again (it’s a recursion after all). Using the fact that \sum_{i=1}^Ni={N+1\choose 2} and \sum_{i=D}^M {\ell \choose D}={M+1 \choose D+1} you can carry out the process a couple more times, and you’ll find that:

\begin{array}{l}S(N,K)=p^K\left[1-{N-2K\choose 1}qp^K+{N-3K\choose 2}\left(qp^K\right)^2\cdots\right]+\left[{N-K\choose 1}qp^K-{N-2K\choose 2}\left(qp^K\right)^2+{N-3K\choose 3}\left(qp^K\right)^3\cdots\right]\\=p^K\sum_{T=0}^\infty {N-(T+1)K\choose T}(-qp^K)^T-\sum_{T=1}^\infty {N-TK\choose T}(-qp^K)^T\end{array}

There’s your answer.

In the approximate (useful) case:

Assume that N is pretty big compared to K. A string of heads (that can be zero heads long) starts with a tails, and there should be about Nq of those. The probability of a particular string of heads being at least K long is pk so you can expect that there should be around E=Nqpk strings of heads at least K long. When E≥1, that means that it’s pretty likely that there’s at least one run of K heads. When E<1, E=Nqpk is approximately equal to the chance of a run of at least K showing up.

Jabberwocky: And that’s why exact solutions are stupid.

Mathematician: Want an exact answer without all the hard work and really nasty formulas? Computers were invented for a reason, people.

We want to compute S(N,K), the probability of getting K or more heads in a row out of N independent coin flips (when there is a probability p of each head occurring and a probability of 1-p of each tail occurring). Let’s consider different ways that we could get K heads in a row. One way to do it would be to have our first K coin flips all be heads, and this occurs with a probability p^{K}. If this does not happen, then at least one tail must occur within the first K coin flips. Let’s suppose that j  is the position of the first tail, and by assumption it satisfies 1 \le j \le K. Then, the probability of having K or more heads in a row in the entire set of coins (given that the first tail occurred at j \le K) is simply the probability of having K or more heads in a row in the set of coins following the jth coin (since there can’t be a streak of K or more heads starting before the jth coin due to j being smaller or equal to K). But this probability of having a streak of K or more after the jth coin is just S(N-j,K). Now, since the probability that our first tail occurs at position j is the chance that we get j-1 heads followed by one tail, so it is p^{j-1} (1-p) . That means that the chance that the first tail occurs on coin j AND there is a streak of K or more heads is given by p^{j-1} (1-p) S(N-j,K). Hence, the probability that the first K coins are all heads, OR coin one is the first tails and the remainder have K or more heads in a row, OR coin two is the first tails and the remainder have K or more heads in a row, OR coin three is the first tails and…, is given by:

S(N,K) = p^{K} + \sum_{j=1,K} p^{j-1} (1-p) S(N-j,K)

Note that what this allows us to do is to compute S(N,K) by knowing the values of S(N-j,K) for  1 \le j \le K. Hence, this is a recursive formula for S(N,K) which relates harder solutions (with larger N values) to easier solutions (with smaller N values). These easier solutions can then be computed using even easier solutions, until we get to S(A,B) for values of A and B so small that we already know the answer (i.e. S(A,B) is very easy to calculate by hand). These are known as our base cases. In particular, we observe that if we have zero coins then there is a zero probability of getting any positive number of heads is zero, so S(0,K) = 0, and the chance of getting more heads than we have coins is zero, so S(N,K) = 0 for K>N.

All of this can be implemented in a few lines of (python) computer code as follows:

An important aspect of this code is that every time a value of S(N,K) is computed, it is saved so that if we need to compute S(N,K) again later it won’t take much work. This is essential for efficiency since each S(N,K) is computed using S(N-j,K) for each j with 1 \le j \le K and therefore if we don’t save our prior results there will be a great many redundant calculations.

For your convenience, here is a table of solutions for S(N,K) for 1 \le N \le 10 and 1 \le K \le 10 (click to see it enlarged):

Posted in -- By the Mathematician, -- By the Physicist, Combinatorics, Equations, Math, Probability | 54 Comments

Q: Aren’t physicists just doing experiments to confirm their theories? Couldn’t they “prove” anything they want?

Posted on July 22, 2010 by The Physicist

The original question was: When we start investigating particles and effects at the quantum level, it seems we are not really measuring the reality of the particles, but rather, our instruments’ reactions to the particles.  So if we calibrated the instruments differently, wouldn’t we get different, perhaps contradictory, results?  It seems that physicists first construct mathematical models, then devise instruments to find just what they are looking for.  That seems to be the same as saying I’m going to make an instrument to find leprechauns, and lo and behold I did it!  Of course, no one can really see the leprechauns, but my instrument says they are there.  You can even make an identical machine and you will detect leprechauns, too.

Physicist: Every observation is nothing more than our instrument’s reactions (Quantum mechanical, or otherwise).
A measurement device that produces foregone conclusions is useless (it provides no new information) so nobody builds them.
While physicists do construct models, and then construct devices to test those models, the primary purpose of the devices is to tear down the models and equations.  Once done, physicists “close the circle” by coming up with new models.
If all we (scientists and Humans too) did was build machines that verified our crazy theories, we’d still be stuck in the stone age, having proven conclusively that everything is controlled by dead people and shamans.

For example: the early mathematical models behind quantum physics and relativity predicted a wide array of very bizarre things (quantum tunneling, super-position, time dilation, stretched spacetime). In an attempt to prove the model wrong (because no one believed it), dozens of different experiments were set up. Every experiment had at least two possible, different results (either disproving, or corroborating the theory).

In fact, this is one of the most basic results from information theory; the more you can anticipate a result, the less information you gain from it.  This is why 6th grade science experiments are pointless (except for edjucation or whatever), and why botched experiments and accidental discoveries are so useful.
As it happens, both the relativity model and quantum model held up to experiment, and so we still use them today.
Conversely, the theory of “luminiferous eather” (the idea that light is a wave in some kind of hidden material) was very popular and held for decades in the late 19th century. However, it wasn’t supported by experiment and so (despite its popularity) it was abandoned.
Admittedly, it’s easy to get tunnel vision with your subject, and even dismiss actual results as statistical noise.

My favorite example is a group of German scientists in the late 19th century who accidentally discovered electron diffraction (proof of the wave nature of electrons) when they were trying to measure the deflection of electrons off of a crystal.  The diffraction effect caused the electrons to come out of the crystal only at a small set of angles, thus saturating the film being used to detect the outgoing electrons at points, instead of smoothly all over.  The German-tunnel-vision-solution?  Buy a “jiggler” to move the film around so that the overexposed points become reasonably exposed blurry patches.

Electron crystalography. It should be bright in the middle and then get dimmer toward to edges. But then stupid quantum mechanics makes everyting all "pointy".

But tendencies like tunnel-vision or “going with what everyone else thinks” are generally overwhelmed by a positive and contrary result.
For example: You could spend your whole life describing, in detail, the physics of a flat world. But the second someone travels all the way around the planet, all of your theories are instantly useless.

Posted in -- By the Physicist, Philosophical, Physics, Skepticism | 1 Comment

Q: What’s up with that “bowling ball creates a dip in a sheet” analogy of spacetime? Isn’t it gravity that makes the dip in the first place?

Posted on July 19, 2010 by The Physicist

The original question was: … also brings up the famous Einstein analogy of a bowling ball in a mattress as bending spacetime. What confuses me is that this seems circular- using the analogy, say we put a bowling ball on a mattress and then roll a marble past it. The marble will fall in towards the bowling ball. But what’s causing it to fall in? Gravity!

Physicist: Here’s what this is about. Way back in the day a popular demonstration used to explain how the presence of matter creates gravity was to drop a heavy ball onto a sheet of some kind, and then roll a smaller ball around the inside of the indentation that is made. If you were to try this demonstration while floating around on the space station you’d be wasting time that could be better spent putting on pants two legs at a time (no gravity to pull the bowling ball and make the indentation in the first place).

In Newtonian mechanics gravity is a spooky, unexplained force. In Einstein’s General Relativity gravity is caused by the curvature and stretching of space and time. Objects move in straight lines like always, but the messed up spacetime they move through makes it appear as though they’re changing direction (that is to say: falling). What’s weird as hell is that they really are moving in straight lines locally, but not globally. If you carefully try to draw a straight line on a bowl you’ll find that it may be straight if you look at a tiny piece of it, but if you stand back it’s curved.

The bowling-ball-mattress thing is another example of how messed up geometry can create “force”. It’s just a bad metaphor. In the one case the pull toward the center is a result of the object in question following a straight line through a messed up spacetime, and in the other it’s trying to roll downhill.
Different.

Posted in -- By the Physicist, Physics, Relativity | 14 Comments