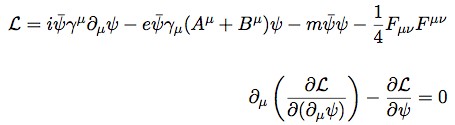Q: If we find a “Theory of Everything” will we be done?

Posted on July 5, 2010 by The Physicist

Physicist: Not even close.

One could even make the argument that finding the theory of everything (often called “unified field theory”) is just the start of the real science.  The theory of everything (TOE) will finally tie together all of the fundamental forces, describe the behavior of every type of particle, and explain in fine detail how space and time behave in all cases.

We’ve seen unifying theories before (not the unifying theory) and they don’t generally answer questions on their own, but merely provide tools to explain things later on down the line.  For example; in several strokes of the quill Newton unified the “make apples fall” force with the “swing planets around” force under the umbrella of “universal gravitation”.

With universal gravitation (which says that gravitational force is: F=\frac{GMm}{R^2}, where M and m are the different masses involved) you can quickly explain why the Moon goes around the Earth, why all orbits are elliptical, and even why planets, Stars, Moons, and the Earth are round.

What you can’t explain, without buckets of math (and often as not: computer power), are things like phase lock, Lagrange points, and why many galaxies have spiral arms.  Even worse, you can’t actually solve problems involving 3 or more objects.  You can exactly write down how two objects will orbit each other, but as soon as there are three, the best you can do is approximation.  This is called the “three body problem”, and it’s likely to remain unsolvable forever.

The Trojan Asteroids float around in two of Jupiter's Lagrange points. This is completely described by the Law of Universal Gravitation, but it still took a lot of work to figure out what was going on. Image stolen from: http://www.dtm.ciw.edu/users/sheppard/satellites/trojan.html

So, a theory of everything, while it would be able to describe the details of how all forces and particles interact on all levels, would still only be a set of equations.  And having the equations is pretty different from having the solutions to those equations, and really different from understanding the implications of those solutions.

The equations required to describe the motion of a particle according to Quantum Electro Dynamics (an extremely accurate theory). Solving these equations is left as an exercise for the reader.

Posted in -- By the Physicist, Physics | 10 Comments

Q: Is it possible to say if the Earth is moving or sitting still without going into space?

Posted on July 3, 2010 by The Physicist

Physicist: Relativity (both Galileo‘s and Einstein‘s) states that the laws of physics will work the same no matter how fast or slow you’re moving, so long as that movement is at a constant speed and in a constant direction.  Galileo talked about boats, and Einstein talked about trains, but it’s all the same stuff.  A point on the Earth, rather than moving in a nice straight line, is being swung around on 3 circles at the same time.  As a result, physics doesn’t work quite the way it should.

One of these circles is the wobble induced by the Moon’s pull.  Rather than thinking that “the Moon orbits the Earth” it helps to think that “the Moon and the Earth orbit their common center of mass”.  The Earth is about 80 times more massive than the Moon, and as such, the center of the Earth-Moon system is about 1,500 km beneath the surface of the Earth (not in space between them), which is why I’m describing the effect as a “wobble”.  This wobble is made apparent by the tides, which would otherwise be very mysterious (where does the force come from?).

The Earth (blue) and the point around which the Earth wobbles (red).

Another circle is the Earth’s orbit around the Sun.  Although they originally didn’t know why, sailors have always been aware that in addition to lunar tides there is a smaller “solar tide” that occurs every day at noon and midnight.  This tide is a symptom of the Earth moving around the Sun, and it’s about 46% as strong as the lunar tide.
Finally, the most dramatic, fastest circle is the Earth’s rotation.  You can tell the difference between the Sun and Moon moving around the Earth, and the Earth spinning because a stationary Earth doesn’t experience “coriolis forces”

Coriolis forces are responsible for large scale weather phenomena like hurricanes, as well as a host of much smaller, more boring effects, like Foucault pendulums.

The direction in which a Foucault Pendulum swings back and forth slowly rotates. In reality, the pendulum is trying to remain swinging in the same direction, but the Earth is turning under it.

So even before knowing the cause, it’s possible to deduce that the Earth is not stationary, because the laws of physics here are not the same as the laws we would observe on a completely stationary object.

Posted in -- By the Physicist, Physics | 4 Comments

Q: Will there always be things that will not or cannot be known?

Posted on June 30, 2010 by The Mathematician

Mathematician: Unfortunately, limits to knowledge seem to be built into the nature of the universe, and even into logic itself.

Relativity: Einstein’s theory of special relativity implies that no information can travel faster than the speed of light. That means that information from sufficiently recent, sufficiently far away events will not have had the time to propagate to us yet, making detailed knowledge of such events impossible. In physics speak, we say that these events are outside of our “past light cone“, “space-like separated” from us, or just “elsewhere”. As long as new events of this type keep happening, there will always be things about which we do not and cannot know.

Quantum Mechanics: The Heisenberg uncertainty principle states that the uncertainty \Delta x we have in a particle’s position and the uncertainty \Delta p we have in the particle’s momentum cannot both be very small at the same time. In particular, the product of these uncertainties is greater than a constant (\Delta x \Delta p > \frac{\hbar}{2}). This implies a fundamental limit to the knowledge that is possible because we can know x accurately or p accurately, but not both.

What’s more, the vast majority of physicists agree that quantum mechanics demonstrates the universe is random at a fundamental level. This means that some events, like the time at which an atom will decay, can be predicted only probabilistically. We can say how likely an atom is to decay in a given time interval, but we will never be able to say precisely when the decay will occur, placing another limitation on what knowledge is possible. (Physicist’s note: After the decay you still can’t say when exactly it happened because according to quantum mechanics the exact time doesn’t actually exist!)

Mathematics: Gödel’s  first incompleteness theorem states (essentially) that any mathematical system  that is able to express elementary arithmetic (and doesn’t contain any contradictions) must contain true arithmetical statements that cannot be proven within that system. Essentially this implies that there will always be true mathematical statements that we cannot prove.


Add to all of these theoretical considerations the enormous (and possibly infinite) number of things that could be known about our physical universe, and the (most definitely) infinite number of true mathematical statements that could be known, and it is clear that there will always be knowledge that is beyond our reach.

Posted in -- By the Mathematician, Math, Philosophical, Quantum Theory, Relativity | 6 Comments

Q: If you could see through the Earth, how big would Australia look from the other side?

Posted on June 27, 2010 by The Physicist

The original question was: Relative to the size my feet appear when I’m standing up and looking at the ground, how large would Australia appear if I could see all the way through the Earth and observe its shape?  Also, if we considered my location to be a new “north pole”, how large would the “northern” hemisphere I observe seem relative to the “southern” hemisphere? In other words, due to the direct inverse relation between apparent size and distance, how much smaller does one half of a sphere appear from a point directly centered on the surface of the other half?

Physicist: This is example of “party trick mathematics”, the kind of math that you can do in your head, but that looks really complicated.  There’s a seriously old theorem from the days when togas meant math (not frat parties) called the “inscribed angle theorem”.  It says that if something has an angle on a circle of 2ϕ when seen from the center of the circle, then when seen from a point on the edge it will have an angle of ϕ.  What’s really surprising is that it doesn’t matter where you are on the circle.  It always works.

The Inscribed Angle Theorem: Surprising, but true.

I estimate that Australia spans about 34°.  Which means that, if you could see it through the Earth, it would take up about 17° of your vision.  Also, it wouldn’t matter where you are on the planet, it would always be 17°.  Unless you’re in Australia.  The size of where ever you are is always 180°.  Unless you’re on the beach or something (90°?).

Lucky for us (people), we all scale about the same.  There are some (literal) rules of thumb that you can use to estimate angles.  From standing, your feet are about 10°.  With your arm outstretched, the width of your thumb is about 1.5°, and your fist is about 7°.

So if you could see Australia through the ground, it would span about two and a half fists-at-arms-length, or a little less than two of your-own-feet-while-standing.  If you could see the other hemisphere (pick one), then it would appear to be exactly 90° across.

What follows is answer gravy:

Finally, for those of you who want to find exact arcangles on the Earth’s surface: If you have two locations at latitudes \gamma and \phi, and the difference in longitudes is \theta, then the true arcangle between them is:

\cos^{-1}{\left(\cos{(\gamma)}\cos{(\phi)}\cos{(\theta)}+\sin{(\gamma)}\sin{(\phi)}\right)}

Also, if you multiply this number by 6365, then you’ve got the distance between those points in km (as the crow flies).

Posted in -- By the Physicist, Brain Teaser, Geometry | 2 Comments

Q: How is it that Bell’s Theorem proves that there are no “hidden variables” in quantum mechanics? How do we know that God really does play dice with the universe?

Posted on June 22, 2010 by The Physicist

Physicist: Bell’s theorem, and its philosophical fallout, is one of the most profound discoveries since relativity.

Bell’s theorem states (among other things) that the universe is fundamentally unpredictable, and that quantum mechanical things (for example: everything) are not actually in one state.  If a box could contain either a blue marble or a red marble, then when you open it you’ll see either one or the other.  In “reality” it was one color or the other before you open the box.  In QM, it can be both before you open the box (it’s actually still both afterwards, but moving on…).

Einstein (and most other physicists of the time) believed that if you knew everything about a system of particles (no matter how big) that you could theoretically predict what that system will be doing in the future, perfectly.  Homeboy thought that the only reason that the movement of air molecules seems to be random, is that we can’t perfectly measure that exact position and velocity of every single one.  So he thought that every particle truly is in some particular state, but that we merely don’t know for sure what that state is (the marble in the box has only one color, but we don’t know what it is).

The idea that randomness and unpredictability are caused by unknown (or unknowable) things is called “hidden variable theory” (The ‘Stein believed in this).  For example; 2, 2, 3, 6, 0, 6, 7, 9, 7, 7, 4, 9, 9, … is not random, but seems random.  It would be really hard to predict the next term (7) if you don’t know the hidden variable.  (BTW, the “hidden variable” is: this is the decimal expansion of 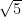\sqrt{5})

Bell’s theorem essentially boils down to a proof that the result of an experiment doesn’t exist until the measurement is made (so it can’t be predicted).  Hidden variable theory presupposes that the particles involved are in definite states, which means that the result of a measurement already exists before the measurement is made.  For example: before you open a gift what you’ll see is already set in stone.  The gift is a set thing before you open the box.  This is not the case for most quantum mechanical systems.

Here’s one of the experiments that demonstrates Bell’s theorem, and two ways to look at it.

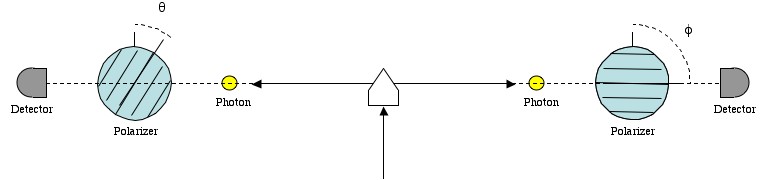
An entangled pair of photons is created and fired in opposite directions. En route the polarizers are randomly oriented, then the detectors measure whether or not the photons pass through. This is done hundreds of thousands of times to measure the relationship between 1) the difference in angles between the polarizers and 2) the probability of measuring the same result.

The experiment: Step 1: Create a pair of entangled photons and fire them in opposite directions.  Entangled particles always yield the same result when they are subjected to the same measurement, and are likely to yield the same result for similar measurements.

Step 2: Randomly orient the polarizers, after the entangled pair is created, but before either is detected (this is hard to time, and is really fast).  This is done so that the photons “don’t know what to expect” and “can’t compare notes”.  Information about polarizer A would have to travel faster than the speed of light to get to photon B before photon B hits it’s own polarizer.  So, without faster than light effects (which don’t exist for many, really good reasons) the photons are each acting independently.  The orientation is random so that the photons can’t “plan ahead”.

Step 3: Measure the polarization.  If the detector “clicks” then the photon made it through the polarizer, and therefore has the same polarization.  If the detector doesn’t click, then the photon had the opposite polarization and was stopped.

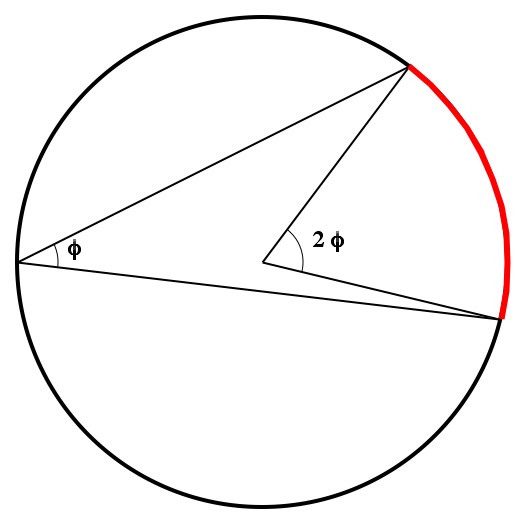
The probability of the measurements being the same (for an entangled pair) is 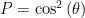P = \cos^2{(\theta)}, where \theta is the difference in angles between the polarizers.  It is tricky to see why, but this probability is impossible if you assume that the result of a measurement exists before the measurement is made.  Here’s why.

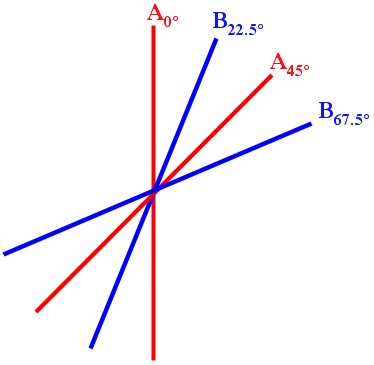
The possible polarizations for polarizer A (red) and polarizer B (blue).

Algebraic approach: Restricting the possible angles of the polarizers to 0° and 45° for A, and 22.5° and 67.5° for B, run the experiment. Here’s what’s about to happen:

1) If you could predict the outcome of each version of the experiment, then you could find a definite value of L (see below).

2) For strictly (unarguable) mathematical reasons L = ±2.

3) Experimentally we find that the average value of L is 2√2.

4) But this is a contradiction, so we cannot actually make useful predictions.

Now it’s happening:

If polarizer A is at 0° and the detector clicks then you’d say “A0 = 1″, and if the detector doesn’t click then “A0 = -1″.  Similarly, you can define B67.5, A45, and B22.5.  Just for the hell of it, take a look at: L = A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5 = (A0 + A45)B22.5 + (A45 – A0)B67.5

L = (A0 + A45)B22.5 + (A45 – A0)B67.5 = ±2, since either (A0 + A45) = ±2 and (A45 – A0) = 0, or (A0 + A45) = 0 and (A45 – A0) = ±2.  So if you could fill out each of these values (A0, A45, B22.5, B67.5), then L = A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5 = ±2 which, notably, is less than or equal to 2.

However, you can’t make all of these measurements simultaneously, so you can’t actually get A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5 for each run of the experiment.  The best you can do is find one of these four terms each time you run the experiment.  For example, if the polarizer A was randomly set to 45° and the detector clicked, and polarizer B was randomly set to 22.5° and the detector didn’t click, then you just found out that A45B22.5 = (1)(-1) = -1 for that run.

You can however find the expectation value by running the experiment over and over and keeping track of the results and polarizer orientation.

E[A0B22.5] + E[A45B22.5] + E[A45B67.5] – E[A0B67.5] = E[A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5] ≤E[|A0B22.5 + A45B22.5 + A45B67.5 – A0B67.5|] = E[2] = 2.

So E[A0B22.5] + E[A45B22.5] + E[A45B67.5] – E[A0B67.5] ≤ 2.  This is one version of “Bell’s Inequality”, and it holds if each term (A0, A45, B22.5, B67.5) has a value.

Using the fact that the chance of getting the same result is 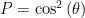P = \cos^2{(\theta)}, and that each term is 1 when the results are the same ((1)(1) or (-1)(-1)), and -1 when the results are different ((1)(-1) or (-1)(1)), you can calculate each term.  For example:

E[A_0B_{22.5}]=P(same)-P(different)=\cos^2{(22.5)}-(1-\cos^2{(22.5)})=\frac{1}{\sqrt{2}}

You’ll find that:

E[A_0B_{22.5}]+E[A_{45}B_{22.5}]+E[A_{45}B_{67.5}]-E[A_0B_{67.5}]=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{-1}{\sqrt{2}}=2\sqrt{2}

Holy crap!  2\sqrt{2}>2!  But that’s a violation of Bell’s inequality!  But the existence of each measurement (whether or not you actually do that measurement) is all you need for Bell’s inequality!  So if the inequality is false, then the result of those measurements don’t exist if the measurement isn’t made!

God plays dice with the universe.

Maybe, if you’re clever and have ready access to a time machine, you could go back and do all the measurements you didn’t make the first time. Then all the results would have to exist! They’d just have to!

Me and my time machine vs. quantum mechanics: If the results exist, but you just didn’t happen to do all the measurements, why not get a time machine?  Then you could do one measurement, go back, do a different measurement, go back, do a different measurement, …  Then every possible result would be known.

However, once again that correlation probability (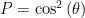P = \cos^2{(\theta)}) screws things up.

So, for example, if the photon goes through at 50°, and then you go back in time, change the polarizer to 51°, and repeat the experiment, then there’s a 99.97% chance (cos2(1°) = 0.9997) that the photon will go through again.

One result from probability says that 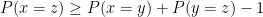P(x=z)\ge P(x=y)+P(y=z)-1.  Do this twice and you get P(w=z)\ge P(w=x)+P(x=z)-1\ge P(w=x)+P(x=y)+P(y=z)-2.  So if you measure in the 0° direction to find A0, then go back and change the angle by 1° and repeat this until you’re measuring at 90°, then:

P(A_0=A_{90})\ge P(A_0=A_1)+P(A_1=A_2)+\cdots+P(A_{89}=A_{90})-89 =90\cos^2{(1^o)}-89=0.9726

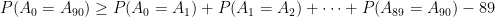
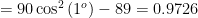
So, if you go back and forth in time to measure whether or not the photon goes through at 1° increments, then there’s a 97% chance that by the time you get to 90° you’ll be getting the same result you did at 0°.  However, in reality 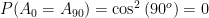P(A_0=A_{90})=\cos^2{(90^o)}=0.

But this is a contradiction.  So the results of each measurement (A0, A1, A2, …, A90) can’t all exist.

If I had to guess, every time you go back in time the experiment is completely reset, and the experiment becomes completely random again.  The reason (such as it is) is below this unsettling picture.

Wait. Wait… Why?

But why?!: It turns out that the reason that the results of a quantum event can’t be predicted, is that every possible result of that event plays out.  So if you ask “will I see the photon go through the polarizer?” the answer is “yes, some versions of you will see the photon go through” and an equally valid answer is “no, some versions of you will not”.

If different versions of you will see every possible result, then the result can’t be predicted, and doesn’t really exist one way or the other until after the measurement is done.  At that time the different versions of you will disagree on the result.  But don’t worry too much.  You’ll never meet you’re parallel-universe twins.

Posted in -- By the Physicist, Philosophical, Physics, Probability, Quantum Theory | 25 Comments

Q: Does an electric field have mass? Does it take energy to move an electric field?

Posted on June 14, 2010 by The Physicist

The original question was: An electric field stores energy.  Energy has mass if I understand E=mc2 correctly.

Now imagine a lone electron. It has an electric field. And therefore that field has mass presumably. If I apply a force to that electron, it will accelerate according to F=ma. My question relates to the m in F=ma.

The electric field must still exist even when the electron is moving. So therefore I am ALSO “moving” the electric field as well as the electron. So the m in F=ma must be made up of two parts, one of which is the mass component of the electric field and one of which just relates to the electron itself? Is that correct or am I confused. PS I appreciate it will be incredibly small and I also appreciate there may also be a magnetic field due to the changing electric field.

Physicist: You’re exactly right.  The electric field has mass (or, at the very least you could say that it has inertia and attracts things gravitationally), because it carries energy.  The energy density, K, of the electric field around a charge, q, is K=\frac{q^2}{R^4} (ignoring all the physical constants for simplicity).  Near the charge (R=0) this equation doesn’t quite work, because the electron isn’t a point, but otherwise it holds up.

You can think of the energy in the field like a mess of Jello™ that’s thick near zero then thins out in all directions.  If you push the charge in the middle, the Jello™ will also move, but the movement will take the form of a jiggly wave that propagates outward.  That wave is where all the extra energy goes.

Electromagnetic energy.

Dropping the metaphor; pushing on a charge generates an electromagnetic (EM) wave.  So applying a force to something with a charge (like electrons) takes more energy than it should (based on the mass alone), because the act of pushing on it generates a spray of photons (which is light, which is EM waves).

Posted in -- By the Physicist, Physics | 10 Comments