The complete question was: What is spectrum? What spectrum does the absolute black body have? Why do different bodies have different spectra? What is spectroscopy and how is it used in science? Why do different elements in star spectrum have different frequencies or what?
Physicist: If you have a sample of light, from a star, or some kind of lamp, or whatever, then its spectrum describes how much of each frequency of light shows up in that sample. For example, a laser has a very “sharp” spectrum (all concentrated at one frequency), while sunlight has a very “broad” spectrum (many frequencies). “Spectroscopy” is the science of gleaning information about something by looking at the spectrum of light it emits, or even absorbs.
The spectrum of a perfectly black body is, not surprisingly, called the “black body spectrum”. The the intensity (I) of light at a given frequency (
) in the black body spectrum is given by 
, where h, c, and k are Planck’s constant, the speed of light, and Boltzmann’s constant respectively.
What’s amazing about this formula is that the only variable is temperature (T). So the spectrum of a perfectly black object is determined entirely by its temperature. The black body spectrum is also a very good approximation for the spectrum emitted by pretty much any thermal source. Such as light bulbs, hot irons, fires, people, stars, etc. In this case light is emitted by atoms slamming into each other and losing energy as light “splashes” off (smacking atoms jiggles their electrons, and jiggling charges is what makes light).
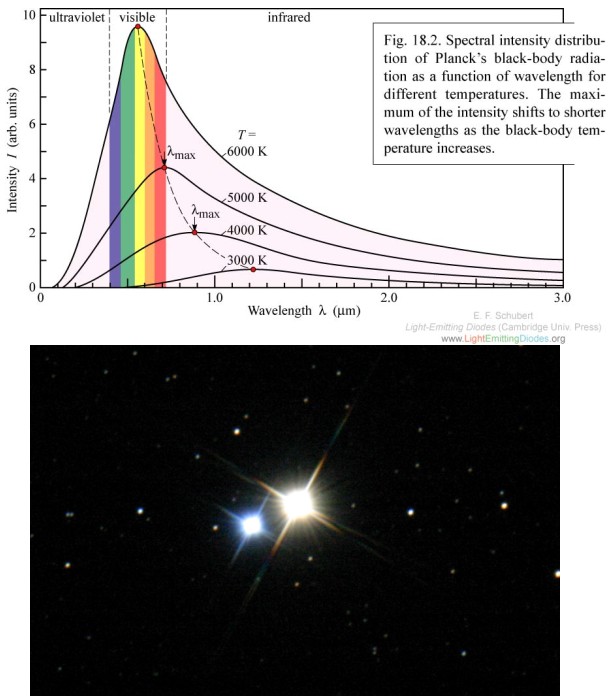
The peak of the black body spectrum moves to higher frequencies as temperature increases. Albireo, a binary star system, is a dramatic example of two different temperatures being indicated by two different colors.
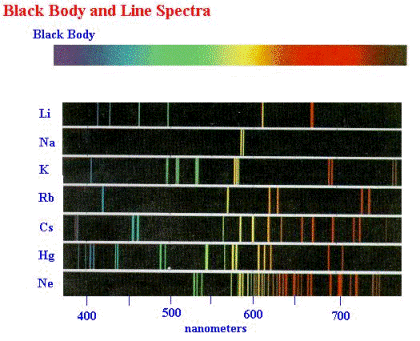
By looking at the spectrum of a light source you can (often) tell what the source of that light is made of, what its temperature is, and even what the light has passed through before it gets to you. The electrons in atoms can only exist in certain, discrete energy levels. As such, the light that they can emit or absorb corresponds exactly to the amount of energy that can be gained or lost by jumping between energy levels. The set of light frequencies that a particular element emits is called that element’s “atomic spectra“.
Left: the spectra of Argon, Helium, Hydrogen, and Mercury. Right: by passing the light through a diffraction grating or prism you can tell what kind of gas is in it.
Different atoms have different spectra because the higher the atomic number, the higher the number of protons in the nucleus, and the greater the pull on the electrons. The electrons in turn stack up and have bizarre magnetic interactions. The interaction between electrons in an atom are very non-linear, and really complicated. So adding one new electron will change the spectrum completely. In fact, beyond hydrogen, the atomic spectra can’t be accurately calculated without a good computer.
Elements also have an “absorption spectra”, that corresponds exactly with emission spectra. For example, big chunks of the infrared light frequencies are in the absorption spectrum of CO2. Hence the famous green house effect.
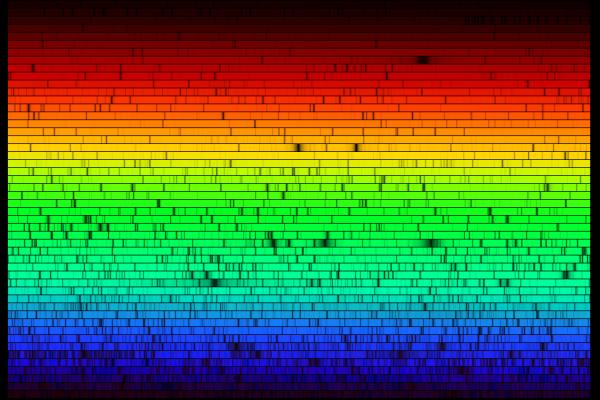
The spectrum of sunlight, as viewed from space (the view is clear from there). Rather than make one long rainbow, this was looped (like text on a page) to save room. The gaps in the spectrum tell us what gases are present in the outer layers of the sun.
Because each element (and molecule) has its own spectrum, we can look at a light source and see immediately which chemicals are present. And by measuring (very carefully) how intense each line is we can tell how much of each chemical is present.
Even slicker, the atomic spectrum of each element is the same everywhere in the universe. So if we look at a star and its hydrogen lines (which tend to be the clearest and most dominant) are all shifted to lower frequencies, then we know that that star must be moving away from us. This is caused by the Doppler effect, and is called “redshift” because the lines look redder.
Spectroscopy is in use here on Earth to quickly determine what substances, and how much, can be found in a sample. Generally by shining light (of a well-known spectrum) through it. For example, you can quickly check ozone levels, humidity, and even the size of particulate pollution, from space by watching sunlight filter through the atmosphere. There are better methods (chemical based measurements) so spectrographic techniques are not en vogue, but they can be used in a pinch.
Also, radar guns and infra-red thermometers are basically spectrometers with a single, specific function.
But the science of spectroscopy is mostly at home in astronomy circles, since they have literally nothing else to work with. Zoologist can smell what they study, electrical engineers can be shocked. But astronomers have to stare at the sky really hard, and measure spectra. Even the discovery of planets around other stars comes down to measuring the red-shifting and blue-shifting of the parent star as its planets make it wobble. We know what interstellar gas and dust clouds are made of by looking at star light filtering through them, and measuring the absorption spectra.
Really, everything we know about stuff outside of the solar system (everything beyond “look, stars!”) is based on spectroscopy.
with some amount of kinetic energy, and leaves 
with the same amount of kinetic energy (conservation of energy). So how can it speed up?
, experienced by the slungshot object is 
, where 
is the incoming speed (from the planet’s perspective), and 
is the angle between the incoming and outgoing trajectories (again from the planet’s perspective). So in general, a sharper angle yields a bigger boost.
