Physicist: Nothing really.
Complex numbers are very useful for streamlining a lot of different types of math, generalizing ideas, and “closing” the real numbers. In quantum theory you’ll find that on the most fundamental level the universe seems to prefer complex numbers to real numbers.
But you can’t use them to count or measure stuff for crap, so most people can live long happy lives without being particularly bothered by complex numbers. If you can call that living.
Mathematician: There are many ways to view complex numbers, but one of the most intuitive is to think of them as representing points in the plane. Doing so will allow us to interpret basic arithmetic operations like addition and multiplication as performing geometric manipulations.
How does this work? Well, every complex number z can be written as  where x and y are real numbers, and i is the square root of -1. We can then think of z as a point on the (x,y) plane with x being the position along the horizontal (i.e. real) axis, and y the position along the vertical (i.e. imaginary) axis. To understand the operation of adding and multiplying complex numbers though, we need to think about them slightly differently.
where x and y are real numbers, and i is the square root of -1. We can then think of z as a point on the (x,y) plane with x being the position along the horizontal (i.e. real) axis, and y the position along the vertical (i.e. imaginary) axis. To understand the operation of adding and multiplying complex numbers though, we need to think about them slightly differently.
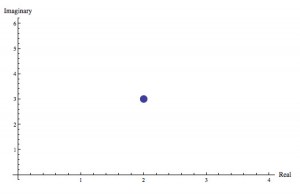
The complex number 2+3i represented as a point in the complex plane. Have you ever seen a more boring image in your life?
If we choose, we can treat complex numbers as vectors rather than points. That means that now  represents not the point (x,y) but rather, the directed line segment which extends from (0,0) in the complex plane to (x,y) in the complex plane (unless otherwise stated we will assume here that our vectors are emanating from the origin (0,0)). You can think of a vector as simply representing a magnitude (or length) and a direction. The line segment extending from (1,2) to (-4,5) is the same as the one extending from (-4,5) to (1,2), but the vectors represented would be different because they would be pointing in opposite directions. Vectors are often drawn as arrows.
represents not the point (x,y) but rather, the directed line segment which extends from (0,0) in the complex plane to (x,y) in the complex plane (unless otherwise stated we will assume here that our vectors are emanating from the origin (0,0)). You can think of a vector as simply representing a magnitude (or length) and a direction. The line segment extending from (1,2) to (-4,5) is the same as the one extending from (-4,5) to (1,2), but the vectors represented would be different because they would be pointing in opposite directions. Vectors are often drawn as arrows.
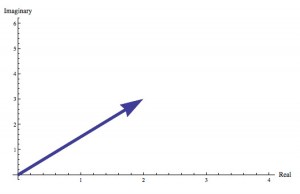
The complex number 2+3i represented as a vector in the complex plane. Compared to our last image, this is a hoot.
Once we have the vector notion of a complex number, we can think about adding complex numbers as adding vectors. For example, if we have

and
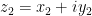
then
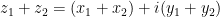 .
.
Hence,  is the vector in the complex plane that extends from (0,0) to
is the vector in the complex plane that extends from (0,0) to 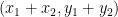 . Note that
. Note that 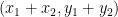 is the point we get to if we piggy back vectors z1 and z2 and then follow them both. By this I mean that we translate (i.e. move without rotating or stretching) z2 so that its beginning is at the end of z1, and then we follow the path consisting of the two vectors until we get to the (new) end of z2. However, since
is the point we get to if we piggy back vectors z1 and z2 and then follow them both. By this I mean that we translate (i.e. move without rotating or stretching) z2 so that its beginning is at the end of z1, and then we follow the path consisting of the two vectors until we get to the (new) end of z2. However, since 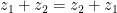 , we can also piggy back z1 at the end of z2 to get the same result. A slightly different view is achieved if we think of our first number
, we can also piggy back z1 at the end of z2 to get the same result. A slightly different view is achieved if we think of our first number  as being a vector, and our second number
as being a vector, and our second number 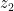 as being a point. In this case,
as being a point. In this case,  simply corresponds to moving the point
simply corresponds to moving the point 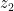 by the distance and direction represented by the vector
by the distance and direction represented by the vector  .
.
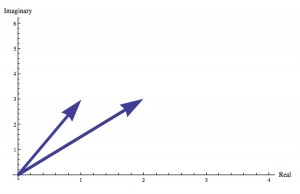
Here are two complex numbers represented as vectors, 2+3i and 1+3i.
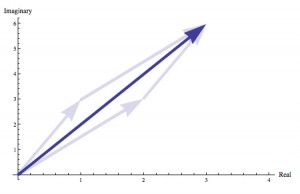
When we sum the complex numbers 2+3i and 1+3i we get the complex number 3+6i.
Alright, so addition of complex numbers can be thought of as adding vectors in the complex plane (or moving a point by the distance and direction stored in a vector), but what the heck does multiplication do? Well, to understand multiplication we need yet another geometric way of thinking about complex numbers.
First though, we make a quick (and relevant) aside. For any complex number z, we have by definition that the absolute value 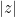 of z satisfies
of z satisfies

which is precisely the formula for the distance between the point (0,0) and the point (x,y). Hence, 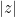 measures the length of the vector that z represents. Now, according to Euler’s formula, we have that for any real number
measures the length of the vector that z represents. Now, according to Euler’s formula, we have that for any real number 
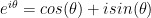 .
.
hence 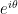 is a complex number since it is the sum of a real and imaginary number. In particular, we have
is a complex number since it is the sum of a real and imaginary number. In particular, we have

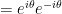
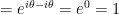
That means that any complex number representable in this form must have a distance of 1 from the origin. In other words, such numbers represent points on the unit circle, or equivalently, vectors of length 1 extending from the origin. As it turns out, all vectors in the complex plane with length 1 can be represented in this form. But what angle does each of these vectors point at? Well, we compute the angle of the line segment (0,0) to (x,y) with respect to the horizontal axis using  . In our case though, since
. In our case though, since  and
and 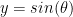 this gives:
this gives:
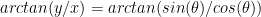
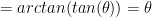 .
.
Hence, the complex number 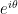 represents a vector of length 1 pointed at angle
represents a vector of length 1 pointed at angle  . Similarly, for any non-negative number r, we have that the complex number
. Similarly, for any non-negative number r, we have that the complex number

represents a vector of length r pointed at angle 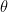 . This provides a new way of thinking about a complex number: as a vector specified by its length and angle. What happens when we multiply two such numbers
. This provides a new way of thinking about a complex number: as a vector specified by its length and angle. What happens when we multiply two such numbers  and
and 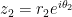 together? Well, we have
together? Well, we have

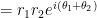 .
.
Hence, 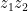 is a new complex number representing a vector of length
is a new complex number representing a vector of length 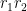 pointed at angle
pointed at angle 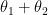 . Therefore, we can think of the action of
. Therefore, we can think of the action of  multiplying
multiplying 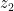 as causing the vector
as causing the vector 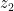 to stretch by a factor of
to stretch by a factor of 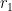 and rotate by an angle
and rotate by an angle  .
.
Hence, to recap, we can view complex numbers geometrically as representing points or vectors in the complex plane. If we do this, then adding complex numbers corresponds to adding together vectors, or equivalently, moving the point that the second complex number represents along the vector that the first complex number represents. On the other hand, we can think of multiplication of complex numbers as corresponding to scaling and rotating the second complex number in the multiplication by the length and angle inherent in the first complex number. Finally, we note that taking the absolute value of a complex number corresponds to measuring the length of the corresponding vector. Therefore, one way to view complex numbers is as a means for converting geometric operations (translation, rotation, scaling) into algebraic operations (adding, multiplication) and back again. As you might imagine, this can be extremely useful!
), which says that you should expect a nice straight line (like the one above).
, which is ugly.