Q: Could the “proton torpedoes” in Star Wars be a thing?

Posted on June 24, 2018 by The Physicist

Physicist: If you’re a fan of Star Wars you may remember proton torpedoes from Episode IV as the only weapon that, when fired down an exposed thermal exhaust port on the Death Star, would “…start a chain reaction which should destroy the station.“, because obviously “The shaft is ray-shielded, so you’ll have to use proton torpedoes.“.

Fans of Star Trek, on the other hand, think they just read “photon torpedoes” twice.

According to the perfectly named Wookieepedia, proton torpedoes release clouds of high energy protons on impact.  Now technically, that’s what all explosives do.  By mass, atoms are almost entirely made of protons and neutrons, each of which are around 2000 times more massive than electrons, and (for most elements) show up in roughly equal numbers.  So about half of the mass of practically anything is protons (the glaring exception is hydrogen, which is 1 proton and 1 electron).

Incidentally releasing clouds of protons, because that’s what’s in clouds of anything, is clearly not the idea behind proton torpedoes nor the spirit of this question.  Neutron bombs (which are real things) release a heck of a lot of neutrons and not too much else.  Proton torpedoes should be like neutron bombs, just with protons.

Once again physics, the queen of sciences and mother of buzzkills, has things to say.  The thing about protons is that long before you notice them doing damage by physically impacting things, you notice their electrical charge.  A proton is like a mosquito when you’re trying to sleep; the mass is not what’s important.

There are incomprehensible electrical charges buried inside of everything, we just don’t notice them because they’re normally almost perfectly balanced.  One gram of protons, without accompanying electrons to bring their net charge to zero, would create an electric field strong enough strip electrons from their host atoms and ionize air more than 15 km away.  It wouldn’t be too healthy for any other materials either; a field this large and intense could pull lightning bolts through granite at a range of 10 km.

If you will not be turned... you will be destroyed!

In the immediate vicinity of this Tesla coil the electric field exceeds the 3kV/mm needed for air to spontaneously ionize (hence the faint glow around the rod).

So a proton torpedo with a one gram payload does a heck of a lot of damage just by existing.  Luke’s aim didn’t really need to be that good.

Ironically, the big effect of detonating the torpedo and releasing the protons is that the electric field actually drops.  As the last post talked about too much, you can understand a lot about electric and gravitational fields by “drawing bubbles” around them.  The total field flowing out of a bubble is proportional to the amount of charge inside of that bubble.  So if you’re standing far enough away, the field you feel stays about the same whether or not the torpedo has exploded.  As the shell of protons expands and repels itself, the field outside of it stays about the same while the field inside of it disappears.  If you’re up close, when the expanding shell of protons passes you (assuming you’re alive) you’d find yourself in a region with little or no electric field.  The most destructive thing you can do with a pile of protons is not blow it up, but keep it together in as small a place as possible.

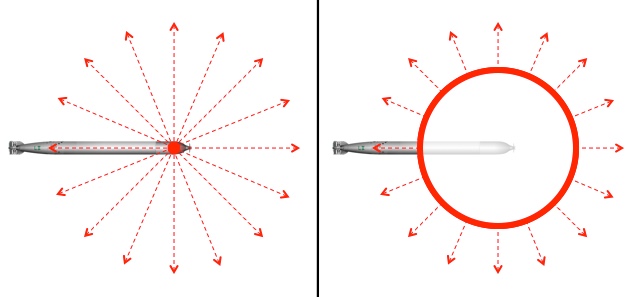
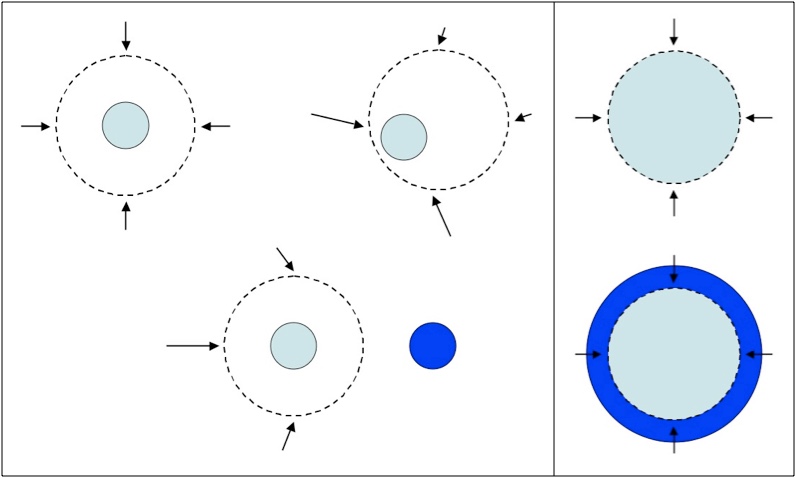
Left: A torpedo (or anything else) with an excess of positively-charged protons produces an electric field.  Right: As the shock front of proton shrapnel expands, the field outside stays about the same while the field inside drops to around zero.

The only way to block the electric field created by a bucket of charge is to surround it with the same amount of the opposite charge.  Both positive and negative charges create electric fields, but those fields counteract each other.  That’s why, despite containing many kg of protons, you doesn’t destroy everything around you.

Unfortunately for BlasTech Industries (famed maker of clumsy, random blasters), counteracting electric fields is exactly what charges always do, given the chance.

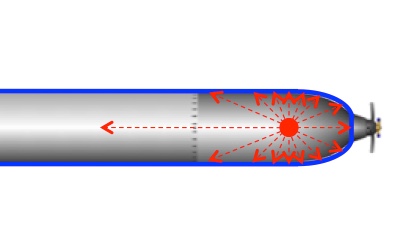
Negative charges (blue) flow toward positive charges (red), because that’s what charges do, until they balance.  Once they do, the net electric field outside the torpedo is zero.

So even if you intentionally store protons in you proton torpedo with the hope of weaponizing its electric field, the first thing that will happen is any nearby matter will ionize.  The loosed electrons will fly toward and coat the torpedo while the stripped nuclei (which are full of protons) beat a hasty retreat.  Assuming the casing is a perfect insulator, in the end you’d have a torpedo with a gram of extra protons inside, about half a milligram of electrons outside (because electrons are about 2000 times less massive than protons), and no devastating electric field.

You could keep the protons and electrons together until the torpedo hits its target, then release the protons but keep the electrons in place (I mean… somehow).  Then you could transport your munitions without preemptively killing everything around them.  But that would be like firing bullets tied to (very strong) rubber bands; the electrons and protons would rather fly back together than do anything else.

So “proton torpedo” may just be a code name like “tomahawk missile” (noteworthy for its lack of tomahawks).  That, or George Lucas is playing a little fast and loose with physics.

Posted in -- By the Physicist, Particle Physics, Physics | 9 Comments

Q: Why does gravity pull things toward the center of mass? What’s so special about the center of mass?

Posted on June 12, 2018 by The Physicist

The original question was: How do you measure d in the equation for universal gravitation (f=\frac{GMm}{d^2})?  It can’t be the distance between the surfaces of the objects, or when they touched f would be “infinite.”  It can’t be the distance between their centers of masses because if I shot a bullet into a rubber ball their centers of mass might coincide, and again d would be zero.  It can’t be the distance between the center of mass of one object and the surface of the other object, because there would be two possible d’s.

Physicist: Nature abhors a singularity.  So when you see a nice glaring one (like this case, where d=0 makes the force jump to infinity) it’s worth pausing to consider how the universe finagles its way out.  When you apply Newton’s Law of Universal Gravitation, f=\frac{GMm}{d^2}, to planets and stars, d is indeed the distance between the centers of mass.  But when to use that standard and why it works is a little subtle.

One of the most important ideas in physics is that the exact same laws apply to everything, everywhere, always.  Nothing and nowhere gets special treatment, and that includes the center of mass.

Nothing is sacred.

The stuff at the center of the Earth does pull on you, but that’s nothing special; so does literally everything else.  Phone books, your worst enemy, that thing you saw that one time, everything on Earth (and otherwise) pulls on you according to Newton’s law.  Every atom pulls on every other atom.

All mass creates gravity and pulls things toward it.  Here on Earth, we always feel a pull toward the center of the Earth (top), so it might seem as though there’s something special down there.  In reality, we’re experiencing the collective pull of everything in and on the Earth (bottom).

The reason you don’t notice a pull toward each individual thing around you is that gravity is weak.  The physical (as opposed to emotional) attraction between you and someone you’re walking next to is a force on the order of the weight of a mote of dust (tens of nanograms).  The air moving in and out of your lungs pushes you around far, far more.

The reason you do notice a pull toward the Earth is that there’s a lot of Earth to do the pulling; around 100,000,000,000,000,000,000,000 times the mass of the person next to you.  Sure it’s farther away (around 4,000 miles on average), but there’s a lot of it.  Heck, it blocks half the sky (the lower half).

Finally, the reason everyone feels a pull toward the center of the Earth is that, for most intents and purposes, the Earth is a perfect sphere.  No matter where you are and no matter how you look at it, you can draw a line through the middle of the Earth and the two sides will be mirror opposites of each other.  As much as one half pulls you to the right, the other pulls you to the left.  The collective pull of both halves is right down the middle; toward the line between them.

The matter on the left side of the (red) line pulls you down and to the left, the matter on the right pulls you down and to the right.  Because the two sides are essentially the same, the “left-and-right-ness” cancel out, leaving a net down.  For a sphere, you can repeat the same argument for any (yellow) line through the center.

The same argument applies to any line that separates the two halves, and all of those lines pass through the center of mass.  Technically, that’s how the center of mass is defined.  So, because the mass of the Earth is spherically symmetric, gravity around here points toward the center of mass.

However!  Gravity does not, in general, point toward the center of mass.  Take for example the Earth-Moon system.  Despite its non-contiguous-ness, it’s still a perfectly legit collection of mass.  The center of mass of the Earth and Moon combined is a point just a little below the Earth’s surface.  That fact is important when you consider how the two orbit each other (the Moon circles that point while the Earth kinda wobbles around it), but it is almost entirely unimportant when you consider how gravity pulls on things presently sitting on Earth’s surface.

The Earth-Moon system to scale.  Notice that gravity does not pull you toward this system’s center of mass (the red dot) it pulls you toward the largest nearby thing (the pale blue dot).

That all said, Earth is only almost perfectly spherical.  You may have noticed that the world is not a perfectly polished ball; there are mountains, oceans, gigatons of missing single socks, and that non-uniformity penetrates well below the surface.  Those variations in the distribution and density of mass means that Earth’s gravity changes (very, very slightly) from place to place, both in magnitude and direction.

Deviations in the strength of Earth’s gravity.  The average surface gravity of Earth is around 980 Gal (1 Gal = 1 cm/s2).  Surface gravity points away from Earth’s center the farthest where the colors are changing the fastest.

By flying a pair of satellites in formation over the Earth and measuring the distance between them we can detect them speeding up and slowing down with respect to each other as one, then the other, passes over differently-gravity’d regions.

The GRACE (Gravity Recovery And Climate Experiment) satellites, cleverly called “GRACE-1” and “GRACE-2”, shot lasers at each other from 2002 to 2017 to measure Earth’s gravity field over that time.  They were so stupefyingly sensitive that they could detect changes in the location of water and ice through the gravity they generate (hence the “climate” part).

Finally, to more directly address the original question, since gravity is a collective pull toward each individual piece of mass and not necessarily a pull toward the center of mass, Newton’s universal law of gravitation has to be applied with a little finesse.  f=\frac{GMm}{d^2} works fine (with d the distance to the center) as long as you’re outside of a sphere of mass, it stops working as soon as you’re inside because the mass above you counteracts the pull of the mass below you.  In the case of a bullet shot through a rubber ball, this is why the gravitational force never jumps to infinity; the equation that says it should ceases to apply.  The universe always has an obnoxious way to get out of having to deal with singularities.

Because gravity is an “inverse square force” (the “d^2” in “f=\frac{GMm}{d^2}” ) it has the remarkable property that the total gravitational field pointing into any closed “bubble” is proportional to the amount of mass contained within that bubble.  Inverse square laws also describe the way light gets dimmer with distance: so if you build a glass bubble around a light source, no matter how big or what shape the bubble is, the same total amount of light flows out of it.

Left: The force through any particular part of the bubble can change, but the total depends only on the amount of mass inside.  Right: If the mass is distributed spherically, then the force is the same everywhere on a spherical bubble (what would make it different?) and we can see why the outer layers of a planet have no impact on the gravity inside of a planet.

The beauty of this is that it allows us to do what should be an arduous calculation (adding up the contribution from every tiny chunk of matter) in a manner that appeals to physicists: stupid easy and deceptively impressive.  One of the immediate conclusions of this is that, as long as you’re outside of the sphere of mass in question, there’s no difference between the gravity of a sphere of mass and the same amount of mass concentrated at a point.  So if the Sun collapsed into a black hole, everything in the solar system would continue to orbit it as though nothing had happened, because the gravity would only have changed below where the surface of the Sun used to be.

The second cute conclusion of this is that if you’re inside of a sphere of mass, only the layers below you count toward the gravity you feel.  So the closer you are to the center, the less mass is below you, and the less gravity there is.  If you were in an elevator that passed through the Earth, you’d know you were near the center because there’d be no gravity.  With the same amount of mass in every direction, every atom in your body would be pulled in every direction equally, and so not at all.  A sort of gravitational tug of war stalemate.

As you approach a sphere of mass gravity increases by the inverse square law, but drops linearly inside the sphere.  If the density varies (which it usually does), that straight line will bow up a bit.

Newton’s Universal Law of Gravitation applies to everything (hence the “universal”).  But instead of applying to the centers of mass of pairs of big objects, it applies to every possible pair of pieces of matter.  In the all-to-common-in-space case of spheres, we can pretend that entire planets and stars are points of mass and apply Newton’s laws to those points, but only as long as we don’t need perfection (which is usually).  As soon as things start knocking into each other, or the subtle effects of their not-sphere-ness become important, you’re back to carefully tallying up the contribution from every chunk of mass.

The pedestal with nothing on it used to have a guy stabbing a bird.  The picture is from here.

The GRACE stuff is from NASA.

Posted in -- By the Physicist, Equations, Philosophical, Physics | 30 Comments

Q: In relativity, how do you define “the observer”?

Posted on May 29, 2018 by The Physicist

Physicist: Whenever you listen to a physicist drone on about relativity (and thank you for your time), you’ll often hear them say things like “…from the perspective of a moving observer…” or “…the observer sees…”.  That’s all very fine and good, but how do you actually define the perspective of that observer?

When you describe something from your own perspective you say things like “it’s ten feet in front of me” or “it’s to my left” or “it passed me by at 30 mph”.  You personally define a set of directions (forward, left, etc.) and distances (however far away something is) relative to yourself.  Far more subtly, your perspective also includes time.  The “future direction” is just as personal and subjective as all of the other direction and distance stuff.  The subjectiveness of time was one of the great insights of Einstein’s relativity.

A short, more pedantic answer is that the observer determines the coordinate system.  That’s just the mathematical way of saying that when you talk about the location and time that things happen, you just describe them in terms of your location and what your watch says.

You are at the origin (center) of a very particular, personal coordinate system.

We’re so accustomed to sharing a coordinate system, like (so called) universal time or latitude and longitude, that it’s easy to fall under the assumption that there really is such a thing as “correct coordinates”.  In reality, such “universal coordinates” are useful only because they’re something a lot of people have bothered to agree on.  And to be fair, it is a lot more useful to tell someone where you are in terms of street corners or latitude and longitude than it is to use your own personal coordinate system, which would amount to saying “I am where I am”.  Philosophically interesting, but not useful.

So while you could describe an observer’s trajectory through a city using some kind of standard coordinate system, that’s not the observer’s perspective.  That’s a description of their location using someone/thing else’s perspective.  Form their own perspective, an observer doesn’t observe their position changing so much as they observe the city moving around them.

As you read this, you would be well within your rights to say “the screen is two feet in front of me” (or however far it is) or more succinctly “the location of the screen is x=2” (where the x direction is forward, the y direction is left, and the z direction is up).  From anyone else’s perspective, the location of the screen is different.  For the person sitting next to you on the subway (if you’re reading this on a subway), the location of the screen might be “x=2 and y=3” or even more succinctly “(2,3,0)”.

If you’ve ever taken an intro physics course, you’ve been subjected to the parable of the guy kicking a ball off a cliff.  The problem is something like “there’s this guy at the top of a 20 m tall cliff who, in a sudden pique of ludophobia, kicks a ball off of the cliff so that it is initially traveling sideways at 3 m/s.  Where does it land?”.  The answer, you will be thrilled to learn, is about 6 m from the base of the cliff.

When you’re setting up this problem you’re faced with an ancient conundrum that has been haunting physicists since long before the age of cartography: what coordinates should I use?  The most correct answer is: whatever lets you be as lazy as possible.

The yellow coordinates are the point of view of the kicker, the red coordinates are the most convenient, and the blue coordinates work fine, but they’re awful.

If you put the center of your coordinates at the base of the cliff, with the axes aligned with the ground and the cliff (red axes in picture above), then one axis gives you height off the ground while the other tells you distance from the cliff.  Very convenient.  In this case the base of the cliff is at (0,0), the ball is kicked at (0,20), and lands in the water at (6,0).  You could use the kicker’s point of view (yellow axes), in which case you would describe the base of the cliff as 20 m below them, and the ball lands 20 m down and 6 m out, (6,-20).

The beauty of physics is that it’s capable of imitating the universe’s supreme deference.  You can write physical laws without ever specifying coordinates, allowing us to define the stage (make up coordinates) and let the universe play out however it likes.  So if you really, really wanted to, you could use completely arbitrary coordinates (blue axes).  But don’t.  The level of the water is no longer just “z=0” or “z=-20”, it’s an equation.  Gravity no longer points in the “negative z direction”, but off to the side.  You can still do the problem and by applying the exact same physical laws, but you have to do a lot more work and that’s categorically unacceptable for a physicist.

In normal space, direction is part of the coordinate system (forward, left/right).  We’re already used to that notion when we talk to each other (as in “You’ve got something on the left side of your face.  No my left, your right.  Well it’s all over the place now.”).  And you already know how to change your coordinate directions.  If you want your “left direction” to become your “forward direction” you just rotate 90° to the left.  If you want your “up” to become your “forward”, just rotate backward 90° (lie down).  Easy.

Observers oriented differently relative to each other will disagree on what directions “forward” (solid lines) and “sideways” (dashed lines) are.

In relativity, the future is just another direction.  Obviously time is a little special.  You can measure distances in any spacial direction using a ruler or string, but to measure “distance” in the time direction you need a clock.  So to define an observer in relativity, you define a coordinate system with them at the center and a time defined by what their clock says.

In relativity, an observer’s personal coordinate system includes their personal time.

It’s hard to picture the “time direction”.  Firstly because it requires thinking in four-dimensional terms and secondly because clocks and rulers are super different.  That’s why physicists futz about with math and coordinates all the time; they allow us to extend our intuition from what we can picture to what we can’t.

It turns out that you can do something similar to changing direction with time.  Exchanging one direction in space for another is called “rotation” (no big deal).  Exchanging one direction in space for the time direction is called a “Lorentz Boost” or, if you don’t speak physicist, it’s called “start moving in that direction”.  Someone facing a different direction relative to you will have a different perspective on what the “forward direction” is and someone moving relative to you will have a different perspective on what the “future direction” is.

Observers moving differently relative to each other will disagree on what directions “future” (solid lines) and “now” (dashed lines) are.

So when you hear things like “when something moves very fast it experiences less time” it’s important to parse out whose time you’re talking about and even what moving means.  This is actually a statement about how things behave in your perspective.  As the observer, time and space are defined relative to your position and clock.  When someone is moving, they’re moving relative to you and according to your coordinate system.  When someone is moving through time slower, it’s according to your clock.  The real headaches kick in when you realize that from the perspective of the other person, you’re the one who’s moving and experiencing time slower.  This feels like a contradiction, but keep in mind that different observers all have their own clocks and coordinates.  There’s a lot more detail on that here.

Here on Earth we’re all moving at about the same speed.  The fastest someone else is likely to be moving relative to you is at most 2000 mph (if you happen to be both on opposite sides of the Earth and on the equator).  Relativistic effects, including disagreeing about time, are only worth talking about when your relative velocities are an appreciable fraction of light’s modest 670,000,000 mph.  The most accurate clocks in the world are capable of detecting disagreements induced by walking slowly (relative velocities of less than 1 meter per second).  But we humans don’t care about differences of a few parts in a quintillion, so while the differences in our clocks are detectable (when we work really hard to detect them), they aren’t worth worrying about.

Posted in -- By the Physicist, Physics, Relativity | 12 Comments

Story Collider

Posted on May 12, 2018 by The Physicist

Physicist: If you happen to be in the LA area this week, I’ll be telling a story for Story Collider about the bizarre, but inspiring experience of doing the “Ask a Mathematician / Ask a Physicist” booth at Burning Man and some of the people we met.

Stranger than you’d think.

It’ll be at the Lyric Hyperion (2106 Hyperion Avenue, Los Angeles, CA) on Tuesday May 15th starting at 8:00pm.  I rarely say a thing will be good times, but this… will be good times.  There will be four other stories I’m looking forward to hearing live, by four other people who I’m humbled to share a stage with.

You can read about the show and get tickets here.

Posted in -- By the Physicist | 3 Comments

For the first time ever, you can buy a book! Again!

Posted on May 8, 2018 by The Physicist

Physicist: For those of you who pre-ordered my book (You’re the real heroes.  Thank you!), you probably got an email from Amazon this morning saying that your order was canceled.

But have no fear, the book is definitely not canceled.  Last year, Springer gave Amazon a rather optimistic publication date, last March 14th, but didn’t bother to update it for several months.  When that time came and went (plus eight weeks) Amazon figured that the book didn’t exist and temporarily pulled the plug.

Bureaucracy’s latest victim: the pre-orders of “Do Colors Exist?: And Other Profound Physics Questions”.

Here’s the good news.  It’s fixed.  You can now pre-order or even re-pre-order through Amazon and the books will be ready to be shipped by May 28th.  I’m speaking to Springer calmly and with measured tone about providing some kind of special deal through this webpage to apologize for this mass canceling.  Until that happens: I’m really, really sorry to everyone this has affected.  Please consider ordering again.

And if it hasn’t affected you; listen, it’s a really good book.  You’d like it.

Posted in -- By the Physicist | 10 Comments

Q: What is the most complicated equation?

Posted on May 2, 2018 by The Physicist

Physicist: If you have plenty of chalkboard space and absolutely nothing better to do, you can write down numbers, letters (Greek if you’re δυσάρεστος), and mathematical operators and eventually you’ll have the longest equation ever written down.  So if you really want to see the most complicated equation ever, call in sick for a few weeks.  A better question might be “what is the most (but not needlessly) complicated equation?”.

There are plenty of equations that are infinitely long, but often they’re simple enough that we can write them compactly.  For example, \pi=4-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}+\ldots  This equation goes on forever, but it’s fairly straight forward: every term you flip the sign and increase the denominator from one odd number to the next.  You can write it in mathspeak as \pi=\sum_{n=0}^\infty(-1)^n\frac{4}{2n+1}.  Like π itself, this sum goes on forever, but it isn’t complicated.  You can describe it simply and in such a way that anyone (with sufficient time and chalk) can find as many digits of π as they like.  This is the basic idea behind “Kolmogorov Complexity“; the length of the shortest possible set of written instructions that can produce a given result (never mind how long it takes to actually compute it).

If you’re looking for an equation that needs to be complicated, a good place to look is physics (I mean, what else do you really need math for?).  If you want to describe the behavior of a ball flying through the air it’s not enough to say “it goes up then down”; there’s a minimum amount of math that goes into accurately calculating the path of falling objects, and it’s more complicated than that.

Arguably, the universe is pretty complicated.  But like π, it is deceptively so (we hope).  If you want to do something like, say, describe the gravitational interactions of every star in the galaxy, you’d do it by numbering the stars (take your time: star 1, star 2, …, star n), determine the position and mass of each, \vec{x}_i and m_i, and then find the force on each star produced by all the others.  In practice this is absurd (there are a few hundred billion stars in the Milky Way, but we can’t see most of them because there’s a galaxy in the way), but the equation you would use is pretty straight forward.  The force on star k is: \vec{F}_k=\sum_{i\ne k}\frac{Gm_km_i}{\left|\vec{x}_k-\vec{x}_i\right|^3}\left(\vec{x}_k-\vec{x}_i\right).  This is just Newton’s law of gravitation, F=-\frac{Gm_1m_2}{r^2}, repeated for every possible pair of stars and added up.  So while the situation itself is complicated, the equation describing it isn’t.  Evidently, if you want an equation that genuinely needs to be complicated, you don’t need a complicated situation, you need complicated dynamics.

The equation for the gravity between many objects is just the equation for the gravity between every pair added up.  Not much more complicated.

The whole point of physics, aside from understanding things, is to describe the rules of the universe as simply as possible.  To that end, physicists love to talk about “Lagrangians”.  Once you’ve got the Lagrangian of a system, you can describe the behavior of that system by applying the “principle of least action“, which says that the behavior of a system (the orbit a planet takes, the path of light through materials, etc.) will always be such that the “chosen” path will have the minimum total Lagrangian along that path.  It’s a cute recipe for succinctly and simultaneously describing a lot of dynamics that would make Kolmogorov proud.

The Lagrangian gives every point on this picture a value and the total along an entire path is the “action”.  The principle of least action says that the path a system will actually take has the least action.  With this principle, a single Lagrangian can be used to derive many physical laws at once, so it’s a good candidate for equations that aren’t needlessly complex.

For example, you can sum up Newton’s physics almost instantly.  Rather than talking about kinetic energy and momentum and falling, you can just say “Dudes and dudettes, if I may, the Lagrangian for an object flying through the air near the surface of the Earth is \mathcal{L}=\frac{1}{2}mv^2-mgz, where m is mass, v is velocity, and z is height”.  From this single formula, you get the conservation of energy, conservation of momentum (when moving sideways), as well as the acceleration due to gravity.  There are also Lagrangians for everything from orbiting planets to electromagnetic fields.

Generally, when you look at the same dynamics applied over and over, the equations involved don’t get much more complicated (although their solutions definitely do).  And if you want to describe the dynamics of a system, Lagrangians are an extremely compact way to do it.  So what’s the most (but not needlessly) complicated equation in the universe?  Arguably, it’s the Standard Model Lagrangian, which covers the dynamics of every kind of particle and all of their interactions.  Notably, it doesn’t cover gravity, but be cool.  It’s a work in progress.

The equation of everything (except gravity).

In some sense this equation is compressed data.  All the relevant dynamics are there, but there’s a lot of unpacking to do before that becomes remotely obvious.  All equations must have some context before they do anything or even mean anything.  That’s why math books are mostly words.  “2+2=4” means nothing to an alien until after you tell them what each of those symbols mean and how they’re being used.  In the case of the Standard Model Lagrangian, each of these symbols mean a lot, the equation itself is uses cute short hand tricks, and it doesn’t even describe dynamics on its own without tying in the Principle of Least Action.  But given all that, it’s describing the most complicated thing we can describe, which is nearly everything, without being needlessly verbose (“mathbose”?) about it.

Answer Gravy: This isn’t part of the question, but if you’ve taken intro physics, you’ve probably seen the equations for kinetic energy, momentum, and acceleration in a uniform gravitational field (like the one you’re experiencing right now).  But unless you’re actually a physicist, you’ve probably never been freaked out by seeing a Lagrangian work.  This gravy is full of calculus and intro physics.

The “action”, S\left(\vec{x}(t)\right), is a function of the path a system takes, \vec{x}(t)=(x_1(t),x_2(t),x_3(t))=(x(t),y(t),z(t)).  More specifically, it’s the integral of the Lagrangian between any two given times:

S\left(\vec{x}(t)\right)=\int_{t_1}^{t_2}\mathcal{L}\left(\vec{x}(t),\dot{\vec{x}}(t)\right)dt

where t1 and t2 are the start and stop times, \vec{x} is a path, \dot{\vec{x}} is the time derivative (velocity) of that path, and \mathcal{L} is some given function of \vec{x} and \dot{\vec{x}}.  If you want to chose a path that extremizes (either minimizes or maximizes) S, then you can do it by solving the Euler-Lagrange equations:

\frac{\partial\mathcal{L}}{\partial x_i}=\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{x}_i}

This is called the Euler-Lagrange equations (plural) because this is actually several equations.  Each different variable (x1=x, x2=y, x3=z) tells you something different.  In regular ol’ calculus, if you want to find the value of x that extremizes a function f(x), you solve \frac{df}{dx}=0 for the value x.  Using the Euler-Lagrange equations is philosophically similar: to find the path that extremizes S, you solve \frac{\partial\mathcal{L}}{\partial x_i}=\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{x}_i} for the path \vec{x}(t).

The Lagrangian from earlier, for a free-falling object near the surface of the Earth, is:

\mathcal{L}=\frac{1}{2}m\left|\dot{\vec{x}}(t)\right|^2-mgz(t)=\frac{1}{2}m\left[\left(\dot{x}(t)\right)^2+\left(\dot{y}(t)\right)^2+\left(\dot{z}(t)\right)^2\right]-mgz(t)

For z:

\begin{array}{l}\frac{\partial\mathcal{L}}{\partial z}=-mg\\[2mm]\frac{\partial\mathcal{L}}{\partial \dot{z}}=m\dot{\vec{z}}(t)\\[2mm]\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{z}}=m\ddot{\vec{z}}(t)\end{array}

So the E-L equation says:

m\ddot{\vec{z}}(t)=-mg or \ddot{\vec{z}}(t)=-g

In other words, “everything accelerates downward at the same rate”.  Doing the same thing for x or y, you get \ddot{\vec{x}}(t)=\ddot{\vec{y}}(t)=0, which says “things don’t accelerate sideways”.  Both good things to know.

You wanna be even slicker, note that this Lagrangian is independent of time.  That means that \frac{\partial\mathcal{L}}{\partial t}=0.  Therefore, applying the chain rule:

\begin{array}{rl}\frac{d\mathcal{L}}{dt}=&\frac{\partial\mathcal{L}}{\partial t}+\sum_i\left(\dot{x}_i\frac{\partial\mathcal{L}}{\partial x_i}+\ddot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\\[2mm]=&\sum_i\left(\dot{x}_i\frac{\partial\mathcal{L}}{\partial x_i}+\ddot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\end{array}

But we have the E-L equations!  Plugging those in:

\begin{array}{rl}=&\sum_i\left(\dot{x}_i\frac{d}{dt}\frac{\partial\mathcal{L}}{\partial \dot{x}_i}+\ddot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\\[2mm]=&\sum_i\frac{d}{dt}\left(\dot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}\right)\end{array}

And therefore:

\frac{d}{dt}\left(\sum_i\dot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}-\mathcal{L}\right)=0

This thing in the parentheses is constant (since it never changes in time).  In the case of  \mathcal{L}=\frac{1}{2}m\left[\left(\dot{x}\right)^2+\left(\dot{y}\right)^2+\left(\dot{z}\right)^2\right]-mgz we find that this constant thing is:

\begin{array}{rl}&\sum_i\dot{x}_i\frac{\partial\mathcal{L}}{\partial \dot{x}_i}-\mathcal{L}\\[2mm]=&\left[\dot{x}\frac{\partial\mathcal{L}}{\partial \dot{x}}+\dot{y}\frac{\partial\mathcal{L}}{\partial \dot{y}}+\dot{z}\frac{\partial\mathcal{L}}{\partial \dot{z}}\right]-\mathcal{L}\\[2mm]=&\left[\dot{x}(m\dot{x})+\dot{y}(m\dot{y})+\dot{z}(m\dot{z})\right]-\left[\frac{1}{2}m\left[\left(\dot{x}\right)^2+\left(\dot{y}\right)^2+\left(\dot{z}\right)^2\right]-mgz\right]\\[2mm]=&\frac{1}{2}m\left[\left(\dot{x}\right)^2+\left(\dot{y}\right)^2+\left(\dot{z}\right)^2\right]+mgz\end{array}

Astute students of physics 1 will recognize the sum of kinetic energy plus gravitational potential.  In other words: this is a derivation of the conservation of energy for free-falling objects.  A more general treatment can be done using Noether’s Theorem, which says that every symmetry produces a conserved quantity.  For example, a time symmetry (\mathcal{L} doesn’t change in time) leads to conservation of energy and a space symmetry (\mathcal{L} doesn’t change in some direction) leads to conservation of momentum in that direction.

Posted in -- By the Physicist, Equations, Math, Physics | 59 Comments