Q: How do Bell pairs (entangled particles) behave experimentally?

Posted on April 20, 2010 by The Physicist

Physicist: When a photon with an unknown polarization hits a polarizer it has a 50% chance of being stopped and a 50% chance of going through.  However, once the photon has passed through a polarizer then its polarization is known (it’s known if it doesn’t pass through as well, but it’s also destroyed).  So if it passes through a vertical polarizer, then it is now definitely vertically polarized, and will pass through additional vertical polarizers no problem (as opposed to being stopped 50% of the time).

A series of identically oriented polarizers in a row is an example of a “repeated measurement”.  One of the phrases that plays on loop in the back of every physicist’s head is “repeated measurements yield the same result”.  This is the sort of thing that refers too.

Two polarizers arranged vertically and arranged diagonally (and perpendicular to each other). The polarizers on the left are a little dark because about half of the ambient light is stopped.

Photons (and particles in general) come in two basic flavors: definite state and indefinite state.  After passing through the first polarizer a photon will be in a definite state (definitely polarized in the same direction as the polarizer).  The spooky thing about indefinite states is that they’re actually in both polarizations at the same time (like Schrödinger’s cat, or particles taking multiple paths in the double slit experiment), as opposed to the polarization merely not being known.  Take a moment to ponder…

Normally the polarization of one photon has nothing at all to do with the polarization of another.  However, by using slickness (there are several methods), photons can be prepared in pairs so that 1) both measurements are the same, and yet 2) both photons are in indefinite states (both horizontal and vertical).

These specially prepared photons are “entangled”.  Entanglement is a property that any particle can have (not just photons), and more complicated forms can be shared by an arbitrary number of particles.

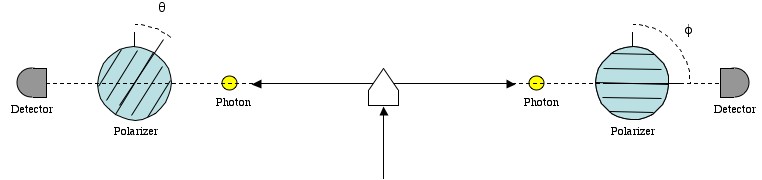
A down-converter (one way to produce an entangled pair) throws two entangled photons in opposite directions. When measured the same way by polarizers, these entangled photons always yield the same result.

Entanglement requires that the particles be in an indefinite state.  If you prepare two photons to be diagonally (\nearrow) polarized (a definite state) then they both have a 50% chance of passing through either a horizontal or vertical polarizer (and 100% chance of passing through a diagonal polarizer like this: \nearrow, and 0% chance of passing through a diagonal polarizer like this: \searrow).  However, if one photon passes through a vertical polarizer, it has no bearing on the other.  They’re in the same state, but they are not entangled.

Entangled photons always give the same result for the first measurement, so long as the two polarizers are oriented in the same direction; both vertical, both diagonal, whatevs.  However, as soon as either photon is measured, you’ll find that they are both in exactly the same (no longer entangled) state.  If you keep measuring the same polarization, the photon will keep going through (repeated measurements).  However, if you start measuring with different orientations, there is no longer any reason for the photons to always give the same result (the way they did when entangled).

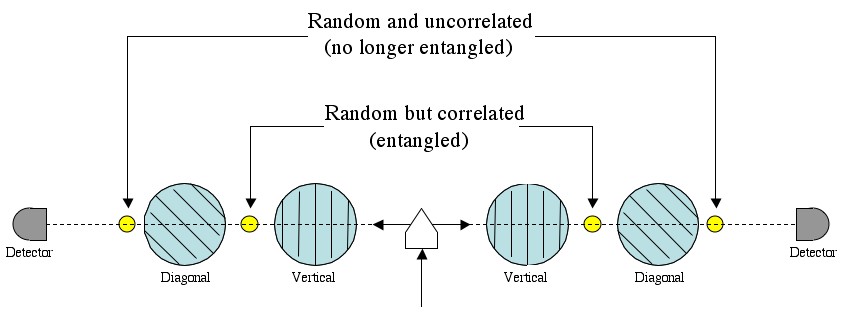
Entangled photons always yeild the same result for the first measurement. However, the first measurement destroys the entanglement. Subsequent, different measurements have random results.

If you want to impress your friends and family with vocabulary, the process of breaking entanglement is called “decoherence”.  It’s the big problem with getting quantum computers off the ground.  I get pretty excited about entanglement and whatnot, so what follows is answer gravy.

How the (fairly easy) math is done:

A photon that is vertically polarized can be written as |\uparrow\rangle and horizontally as |\rightarrow\rangle.  This weird looking notation doesn’t mean anything profound.  It’s basically saying “look! some kind of quantum state!”  As it happens, a diagonally polarized photon can be described as |\nearrow \rangle = \frac{|\uparrow \rangle + |\rightarrow \rangle}{\sqrt{2}} which is just a technical way of saying “up and to the right is half up and half to the right”.  The other diagonal polarization is |\nwarrow\rangle=\frac{|\uparrow\rangle+|\leftarrow\rangle}{\sqrt{2}}=\frac{|\uparrow\rangle-|\rightarrow\rangle}{\sqrt{2}}.

The chance of finding a photon described by | \Psi \rangle in a state | \Phi \rangle is given by P = | \langle \Phi | \Psi \rangle |^2 = \cos^2{(\theta)}, where \theta is the angle between the two states.  For example, the chance of finding a vertically polarized photon in the horizontal state is P = | \langle \rightarrow | \uparrow\rangle|^2 = \left| \cos{(90^o)} \right|^2 = 0 = impossible, which is what you would expect.  The chance of a diagonally polarized photon being detected as vertical is P=|\langle\uparrow|\nearrow\rangle|^2=\cos^2{(45^o)}=\left(\frac{1}{\sqrt{2}}\right)^2=\frac{1}{2}.

Another way of doing exactly the same thing is: P = | \langle \uparrow | \nearrow\rangle|^2 = | \langle \uparrow | \left( \frac{\uparrow\rangle + | \rightarrow \rangle}{\sqrt{2}} \right)|^2 = | \left( \frac{\langle \uparrow | \uparrow\rangle + \langle \uparrow | \rightarrow \rangle}{\sqrt{2}} \right)|^2 = \left(\frac{1 + 0}{\sqrt{2}}\right)^2 = \frac{1}{2}

Now say you have two photons (A and B) that are vertically polarized, you’d write it this way: | \uparrow \rangle_A | \uparrow \rangle_B

Where the A and B subscripts indicate which particle you’re talking about in that bracket.

Here’s how you would write the state of two diagonally polarized photons:

|\nearrow\rangle_A|\nearrow\rangle_B=\left(\frac{\uparrow\rangle_A+|\rightarrow\rangle_A}{\sqrt{2}}\right)\left(\frac{\uparrow\rangle_B+|\rightarrow\rangle_B}{\sqrt{2}} \right)=\frac{1}{2}\left(|\uparrow\rangle_A|\uparrow\rangle_B+|\uparrow\rangle_A|\rightarrow\rangle_B+|\rightarrow\rangle_A|\uparrow\rangle_B+|\rightarrow\rangle_A|\rightarrow\rangle_B\right)

Holy crap!  This is just another way of saying that the chance of measuring any combination of vertical and horizontal polarization is equal.  Check it!  The probability of A being vertical and B being horizontal is:

|\left( \langle \uparrow |_A \langle \rightarrow |_B \right) \left( | \nearrow \rangle_A | \nearrow \rangle_B \right) |^2 = | \frac{1}{2} \left( \langle \uparrow | \uparrow\rangle_A \langle \rightarrow | \uparrow\rangle_B + \langle \uparrow | \uparrow\rangle_A \langle \rightarrow | \rightarrow\rangle_B + \langle \uparrow | \rightarrow\rangle_A \langle \rightarrow | \uparrow\rangle_B +\langle \uparrow | \rightarrow\rangle_A \langle \rightarrow | \rightarrow\rangle_B \right) |^2 = | \frac{1}{2} \left( 1 \cdot 0 + 1 \cdot 1 + 0 \cdot 0 + 0 \cdot 1 \right) |^2 = | \frac{1}{2} |^2 = \frac{1}{4}

Notice that the “A” parts and the “B” parts leave each other alone.

Now here’s an example of a Bell state:

\frac{1}{\sqrt{2}} \left( | \uparrow \rangle_A |\uparrow \rangle_B + |\rightarrow \rangle_A |\rightarrow \rangle_B \right)

(For succinctness you can write this: \frac{| \uparrow \uparrow \rangle + |\rightarrow \rightarrow \rangle}{\sqrt{2}}, just be careful to keep track of which is A and which is B.)  This says that the chance of both photons being vertically polarized is 1/2, and the chance of both of them being horizontally polarized is also 50%.  Even though this Bell state looks like diagonal polarization, it’s not.  A diagonal state is definite:

\frac{|\uparrow \rangle + |\rightarrow \rangle}{\sqrt{2}} = |\nearrow \rangle

If you measure this using vertical/horizontal polarizers you’ll find that the photon has a 50/50 chance of passing through, which seems like an indefinite state.  However, using diagonal polarizers you’ll find that this is definitely a “upright/downleft” polarized photon.

If you rewrite the Bell state in terms of diagonal states (right now it’s written in terms of vertical/horizontal states) you get:

\frac{1}{\sqrt{2}} \left( | \uparrow \rangle_A |\uparrow \rangle_B + |\rightarrow \rangle_A |\rightarrow \rangle_B \right) =\frac{1}{\sqrt{2}}\left[\left(\frac{|\nwarrow\rangle+|\nearrow\rangle}{\sqrt{2}}\right)_A\left(\frac{|\nwarrow\rangle+|\nearrow\rangle}{\sqrt{2}}\right)_B+\left(\frac{-|\nwarrow\rangle+|\nearrow\rangle}{\sqrt{2}}\right)_A\left(\frac{-|\nwarrow\rangle+|\nearrow\rangle}{\sqrt{2}}\right)_B\right] = \frac{1}{2\sqrt{2}} \left[ \left(| \nwarrow \rangle + | \nearrow \rangle \right)_A \left(| \nwarrow \rangle + | \nearrow \rangle \right)_B + \left(-| \nwarrow \rangle + | \nearrow \rangle \right)_A \left(-| \nwarrow \rangle + | \nearrow \rangle \right)_B \right] = \frac{1}{2\sqrt{2}} \left[ | \nwarrow \rangle_A | \nwarrow \rangle_B +| \nwarrow \rangle_A | \nearrow \rangle_B + | \nearrow \rangle_A | \nwarrow \rangle_B + | \nearrow \rangle_A | \nearrow \rangle_B +| \nwarrow \rangle_A | \nwarrow \rangle_B -| \nwarrow \rangle_A | \nearrow \rangle_B - | \nearrow \rangle_A | \nwarrow \rangle_B + | \nearrow \rangle_A | \nearrow \rangle_B \right] =\frac{1}{2\sqrt{2}}\left[|\nwarrow\rangle_A|\nwarrow\rangle_B+|\nearrow\rangle_A|\nearrow\rangle_B+|\nwarrow\rangle_A|\nwarrow\rangle_B+|\nearrow\rangle_A|\nearrow\rangle_B\right] = \frac{1}{\sqrt{2}} \left[ | \nwarrow \rangle_A | \nwarrow \rangle_B + | \nearrow \rangle_A | \nearrow \rangle_B \right]

So the Bell state will also always yield the same result for both photons when measured diagonally.  Isn’t that weird?

Now say you fire a pair of entangled photons in this state at a pair of vertical polarizers.  If one goes through, they both go through and you’re left with a definite state:

\frac{| \uparrow \uparrow \rangle + |\rightarrow \rightarrow \rangle}{\sqrt{2}} \quad \longrightarrow \quad | \uparrow \uparrow \rangle

Which in terms of diagonal states is:

| \uparrow \uparrow \rangle = \left( \frac{|\nwarrow \rangle + |\nearrow \rangle}{\sqrt{2}} \right) \left( \frac{|\nwarrow \rangle + |\nearrow \rangle}{\sqrt{2}} \right) = \frac{1}{2} \left( |\nwarrow \nwarrow \rangle + |\nearrow \nwarrow \rangle + |\nwarrow \nearrow \rangle + |\nearrow \nearrow \rangle \right)

Which means an equal chance of any combination of measurements!  No correlation!  No entanglement!  That mother decohered!

By the by, for fermions (which includes protons, neutrons, and electrons) the important state is “spin”, not polarization.  And for fermions the probability of a particle which is known to be in the state | \Psi \rangle being measured in state | \Phi \rangle is P = \left| \langle \Phi | \Psi \rangle \right|^2 = \left[ \cos{(\frac{\theta}{2})} \right]^2, where \theta is the angle between the axis of the spins.  Without going into detail, the \frac{\theta}{2} term is essentially due to the “half integer spin” of fermions, as opposed to the “integer spin” of photons.

Posted in -- By the Physicist, Physics, Quantum Theory | 13 Comments

Video: What your Spiritual Guru Never Told you about Quantum Mechanics

Posted on April 18, 2010 by The Mathematician

AskAMathematician.com presents a lecture on Quantum Mechanics given as part of Nerd Nite (NYC):

Quantum Mechanics has been around since the thirties and is the basis of essentially all of modern physics. It is a clean theory and has been tested, retested, and verified more than any other physical theory in history. However, some of the basic ideas involved are a little weird, unintuitive, seemingly impossible, and philosophically repugnant. For decades, cults, spiritual healers, and the like have taken the weirdness of actual quantum physics and spun it into fake ideas like “Quantum Consciousness,” “Quantum Healing,” and (sorry to say) “Quantum Leap.” In this talk we will go over some of the misconceptions, the original experiments that led to them, and also how these ideas are applied today and (hopefully) will be in the future.

Entire talk in Power Point format:

Download What Your Spiritual Guru Never Told You About Quantum Mechanics Power Point File

The video comprising part 1 of the 3 parts of the lecture:

The video comprising part 2 of the 3 parts of the lecture:

The video comprising part 3 of the 3 parts of the lecture:

Further Information:

Physicist: If you’re here because of Nerd Nite, welcome!  This is to round off what didn’t get covered.  And for everyone else; check this out!

For more on Quantum Seeing in the Dark, here’s a Scientific American article about the technique, and also how to make it spooky and awesome using the quantum zeno effect:

research.physics.illinois.edu/qi/photonics/papers/kwiat-sciam-1996-nov.pdf

This here is a cavalcade of information about quantum non-locality, and the relevant experiments.  Turns out causality is just a suggestion:

http://www.dhushara.com/book/quantcos/qnonloc/qnonloc.htm

Holy crap!  A different, and difficult to follow, presentation on Quantum Information Theory, the Shor Algorithm, and Hipsters!

Right Here

Posted in -- By the Physicist, Physics, Quantum Theory, Skepticism, Videos | 1 Comment

Q: How big does an object have to be to gravitationally attract a Human or have a molten core?

Posted on April 17, 2010 by The Physicist

The original question was:

I was reading up on Hyperion, Saturn’s moon, and one of the least dense objects in the solar system, and it hit me – what is the critical point for gravity to attract a human? In other words, if you were to make a big pile of rocks in space, at what mass would they drag a human towards them?  And if you kept adding rocks to the pile, at what mass would a heap of rocks create a hot molten core?

Physicist: The answer to the first question is a bit smart-assed.  The object needs to be bigger than you, or (most people would say) you’d be attracting it.  No matter how small an object is, if it has mass, it has gravity.  Another question might be, “How big does something have to be so that you can’t jump off of it?”  It turns out that it needs to be fairly big.  The Little Prince would have gone flying off of his planet if he so much as twitched.

"The Little Prince". Bullshit.

Even Deimos (the smaller of Mars’ two moons) has an escape velocity of only about 12.5 mph, so with a good running start you could literally jump into space.  I figure 12.5 mph is about the fastest that most people can muster in a pinch, so Deimos is about the smallest object that can hold people down, at about 8 miles across (8 miles on average, due to lumpiness).

It’s worth mentioning that “running” on something as small as Deimos is impossible.  With a gravitational pull of about 0.04% of Earth’s, the difference between Deimos’ gravity and zero gravity is academic.  You could easily pogo-stick on your pinky, and it would take so long to fall that you might lose track of which direction is down while waiting for the ground.

The main reason the size of an object is important to its core-moltenness, is because smaller objects radiate heat faster (proportionately) than larger objects, and larger objects have more nuclear fuel to work with.

As far as molten cores go, there are three main sources of heat: formation heat, tidal forces, and radioactive decay.

Tidal forces on a moon are similar to the crushing forces acting on an egg rolled on a table. In the case of Europa the end result is also similar.

Formation heat is just the left over energy you get when you let a few trillion gigatons of stuff fall together.  The formation heat of everything in the solar system was exhausted billions of years ago (except for Jupiter, which continues to slowly deflate and release heat.  Essentially it’s too fluffy).

Tidal forces only really apply to inner moons around gas giants.  The tidal forces have to be huge in order to melt the core just by “massaging” the moon in question.

The most important thing for a liquid core is a supply of radioactive material.  Given the amount of radioactive stuff left in the solar system today (it’s been draining away for the last 5 billion years) an object needs to have a mass between about 1 x 1023 kg and 3 x 1023 kg (between 0.02 and 0.05 Earths, or around 70 million “Deimoses”), give or take.

So age, size, tidal forces, and density are just some of the many variables that go into whether or not a core will be molten.  In fact, given enough time Earth’s core will eventually run out of nuclear fuel and solidify.  But don’t get too concerned, the Sun should swell up and swallow us long before then.

Posted in -- By the Physicist, Physics | 52 Comments

Video: The Scientific Investigation of Aliens – Evidence Examined

Posted on April 14, 2010 by The Mathematician
This talk given at Nerd Nite (NYC) by the Mathematician discusses some of the evidence that has been proposed for the idea that technologically advanced aliens have already arrived on earth, including UFO photographs, crop circles, and abduction stories.

The PowerPoint presentation of this lecture, including references:

Download the Scientific Investigation of Aliens PowerPoint Presentation

Part 1 of the video of this lecture:

Part 2 of the video of this lecture:

References:

Polls

Roper Poll Survey 1999 :

http://www.ufoevidence.org/documents/doc850.htm

Public Opinion Polls on UFOs :

http://www.ufoevidence.org/topics/PublicOpinionPolls.htm

CNN/TIME Poll 1997 :

http://www.cnn.com/US/9706/15/ufo.poll/

Gallup Poll 2005:

http://www.gallup.com/poll/19558/Paranormal-Beliefs-Come-SuperNaturally-Some.aspx

Hallucination Poll Data :

“Prevalence of hallucinations and their pathological associations in the general population”, 2000 by Maurice M. Ohayon

Crop Circles

The International Crop Circle Database :

http://ccdb.cropcircleresearch.com/index.cgi

Why Crop Circles Can’t Be Hoaxed :

http://theconversation.org/booklet2.html

Abductions

Hill Abduction:

http://en.wikipedia.org/wiki/Betty_and_Barney_Hill_abduction

Kenneth Arnold UFO Sighting:

http://en.wikipedia.org/wiki/Kenneth_Arnold_unidentified_flying_object_sighting

Susan Blackmore on Aliens :

http://www.susanblackmore.co.uk/journalism/ns94.html

John Edward Mack :

http://en.wikipedia.org/wiki/John_Edward_Mack

Astronomy

Number of Planets in the Galaxy :

http://en.wikipedia.org/wiki/Extraterrestrial_life

Number of Galaxies in the Universe :

http://imagine.gsfc.nasa.gov/docs/ask_astro/answers/021127a.html

Number of planets in our galaxy :

http://www.madsci.org/posts/archives/2000-01/948204035.As.r.html

Meteorites :

http://en.wikipedia.org/wiki/Meteorite#Fall_phenomena

Other Info

Photo Tampering Throughout History :

http://www.cs.dartmouth.edu/farid/research/digitaltampering/

Alien Abduction Insurance:

http://en.wikipedia.org/wiki/Alien_abduction_insurance

Alien Abduction Insurance Articles :

http://www.alienabductioninsurance.com/articles.html

Aliens and Children :

http://www.aliensandchildren.org/

Developments in Crop Circles Over Time :

http://www.cropcircles.net/

Top 10 Controversial pieces of evidence for extraterrestrial life :

http://www.newscientist.com/article/dn9943-top-10-controversial-pieces-of-evidence-for-extraterrestrial-life.html

The Drake Equation :

http://en.wikipedia.org/wiki/Drake_equation

The Flake Equation :

http://xkcd.com/718/

UFOs :

http://en.wikipedia.org/wiki/UFO

Causes of Hallucinations :

http://www.wrongdiagnosis.com/h/hallucination/causes.htm#causeslist

Crop Circle :

http://en.wikipedia.org/wiki/Crop_circle

Sleep Paralysis :

http://en.wikipedia.org/wiki/Sleep_paralysis

Water Bears :

http://en.wikipedia.org/wiki/Water_bear

Videos

Best of UFOs (part 1) :

http://www.youtube.com/watch?v=6XXOvUwr2YU

Documentaries About Aleins :

http://www.hyper.net/ufo/video-documentaries.html

Crop Circle Being Made (Schofields Quest – Doug Bower 1994) :

http://www.youtube.com/watch?v=XkGbnUXfh4U

UFO sighting (part 2/3) :

http://www.youtube.com/watch?v=-iVYCYjso-U&feature=player_embedded

National Geographic Crop Circles :

http://video.nationalgeographic.com/video/player/science/weird-science-sci/uk_cropcircles.html

Why people believe strange things:

http://www.ted.com/talks/michael_shermer_on_believing_strange_things.html

Photos

Best UFO Photos:

http://www.ufocasebook.com/bestufopictures.html

Strange Flying Machines Slideshow :

http://www.slideshare.net/webtel125/strange-flying-machines-presentation-793157

UFO Photo Competitions :

http://fx.worth1000.com/contests/8300/sightings-7

Circle Makers :

http://www.circlemakers.org/totc2007.html

UFO Drawings :

http://www.ufo-blog.com/ufo-blog/2010/02/sketches-from-fifth-tranche-of-mod-ufo.html

Three spooky UFO vidoes :

http://www.youtube.com/watch?v=7WYRyuL4Z5I

UFO Haiti :

http://www.youtube.com/watch?v=up5jmbSjWkw

List of Military Aircraft in the United States :

http://en.wikipedia.org/wiki/List_of_military_aircraft_of_the_United_States

Balloon Boy Balloon :

http://s2.hubimg.com/u/1922877_f520.jpg

Sun Dogs:

http://en.wikipedia.org/wiki/Sun_dogs

Lenticular Clouds :

http://en.wikipedia.org/wiki/Lenticular_cloud

Photoshopped Images :

http://www.funnydb.com/Pictures/Celebrities/mona_diesel-3320.html

Books

The Demon Haunted World by Carl Sagan :

http://www.amazon.com/Demon-Haunted-World-Science-Candle-Dark/dp/0345409469


Posted in -- By the Mathematician, Astronomy, Skepticism, Videos | Tagged , , , , , , , , , , , , , , | 1 Comment

Q: How do I count the number of ways of picking/choosing/taking k items from a list/group/set of n items when order does/doesn’t matter?

Posted on April 12, 2010 by The Mathematician

Mathematician: Suppose that we have a list containing three items, {A,B,C}, and we want to know how many different ways there are of choosing two items from this list. If we care about the order that items are selected from the list, then the possibilities are

{A,B}, {A,C}, {B, A}, {B, C}, {C,A}, {C,B}

(where {A,B} here means that we’ve selected item A and then item B from the list {A,B,C} ) so the answer is that there are six possible ways of choosing two items out of three. If on the other hand we don’t care about what order the items were selected in (so {A,B} is considered the same as {B,A}) then all the possible unique arrangements are

{A,B}, {A,C}, {B, C}

so the answer is that there are three possible ways of choosing two items out of three when order doesn’t matter.

When there are small numbers of items, it isn’t difficult to just write down all the possible combinations (when order doesn’t matter) or permutations (when order does matter). But what do we do when there are larger numbers of items? For example, it turns out there are 15,504 different ways to choose 5 items out of 20 (when the order of items selected doesn’t matter), far too many to write down. In cases like these we want to use a formula that depends only on n (the number of items in our set) and k (the number of items we will be selecting from it) that can quickly give us the answer we need. Let’s see if we can figure out what this formula should be.

For the time being we are going to assume that the order we select items in does matter (so the selection of A followed by the selection of B is not the same as the selection of B followed by the selection of A). Now notice that since we have n items in total, there are n choices for the first item that we pick. Once we’ve chosen the first item, there are n-1 items left in our list, so for our second selection we have n-1 possible choices. The number of total possible ways of choosing the first two items is therefore n * (n-1) because for each of the n first items we could choose we have n-1 second items possible. Now, for the 3rd item selected there are n-2 items left in the list (since we’ve already used up 2 items out of a total of n), which means that in choosing three items there are a total of n (n-1) (n-2) possible permutations. This pattern continues for each of the k items we are choosing, so that we find that the total number of ways of choosing k items is

(n)(n-1)(n-2)…(n-k+2)(n-k+1)

which can be written using the factorial function as

\frac{n!}{(n-k)!}

Remember however that in this analysis the order of the items selected made a difference. If what we are interested in is the number of ways of choosing k items from a list of n such that order does NOT matter (i.e. in each selection all that matters is which items are in that selection, not which order those items were chosen) then we have to adjust our formula somewhat by making the following considerations.

If we are going to be choosing k items, then how many different orderings of those k items exist? Well, there are k possible choices for which item goes first. After we have chosen which one goes first, there are k-1 that can go second. This leads to a total number of k*(k-1) arrangements for the first two items. Then, there are k-2 items to choose from for the 3rd item, and so on, leading to k*(k-1)*(k-2)*(k-3)*…*3*2*1 total arrangements. Note though that this is just the same as the definition of k factorial, so we just write k! to represent the expression. Now, we observe that the number of ways to choose k items from n such that order matters is k! times bigger than the number of ways to choose k items from n where order doesn’t matter. The reason is because for each of the ways we can make a selection of k items when order doesn’t matter, there are k! different orderings in which we could have chosen each of our k selected items. Hence, since there are  \frac{n!}{(n-k)!} possible choices when order matters, but this is k! times greater than the case when order doesn’t matter, we have that the total number of different possible selections when order doesn’t matter is just given by

\frac{n!}{k! (n-k)!}

This happens to be the definition of what is called the “choose function”, sometimes known as the binomial coefficient or pascal’s triangle, which mathematicians write as {n\choose k}.

Now, to put our work into action. Let’s suppose that we have ten salad ingredients (peppers, avocado, pears, walnuts, beans, peas, corn, croutons, soy beans and olives) and we want to know how many distinct salads can be made using just two ingredients. Well, if our salad is mixed up, then it doesn’t matter what order we put the ingredients in, so this is equivalent to the problem of asking how many ways there are to select two items from a list of ten when order doesn’t matter. This is given by

10 \choose{2} = \frac{10!}{2! (10-2)!} = \frac{(10)(9)(8!)}{(2)(8!)} = \frac{10*9}{2}=5*9 = 45

so there are 45 two ingredient salads you can make from ten ingredients. How many distinct salads can you make that have anywhere from 2 to 10 of our ingredients? The answer is just the number of two ingredient salads plus the number of three ingredients salads plus the number of four ingredient salads, etc. up to the number of ten ingredient salads. In mathematical notation, this is

10 \choose{2} + 10 \choose{3} + {10\choose 4} + …  + 10 \choose{9} + 10 \choose{10}

= 45 + 120 + 210 + 252 + 210 + 120 + 45 + 10 + 1  = 1013

which is simply the number of salads with two or more ingredients that could be made from our ten ingredients.

Posted in -- By the Mathematician, Combinatorics, Math | 11 Comments

Q: Who would win in a fight: Gödel or Feynman?

Posted on April 1, 2010 by The Physicist

Physicist: Both Godel and Feynman had an amazing ability to understand the most fundamental workings of reality, staring unblinkingly into the infinite unknown.  The real question is; who could stare unblinkingly into the infinite fist of a beat-down?

Feynman: More than Human. Godel: Obviously a supervillain.

One of the little known facts about Feynman is that he was a proficient bongo player, which leads me to suspect that he could probably land some solid combos. Also, when shit goes down, who do you call?  Feynman.  When Challenger blew up?  Feynman.  When no one could build a nuke?  Feynman.  What happens when quantum field theory doesn’t adhere to causality?  Feynman ain’t shook.  Somebody help, there’s a kitten locked in this safe!  I shit you not, Feyman’ll crack it.  Bad ass.

Gödel on the other hand is no stranger to talking shit to everybody.  His incompleteness theorem has made him one of the most reviled mathematicians ever.  After his doctoral thesis on how everybody is wasting their time (the “Incompleteness Theorem”) and may as well give up, he was called “Jerk of the year” by most of the mathematical and scientific community.  His response?  “Prove it.”  Also, his ass was crazy.  Like “you punch me in the face and I’ll bite your hand” crazy.  What did he do when he figured out that aliens and unseen government forces were conspiring to poison him?  He made his wife eat his food first.

In a fair fight Feynman would win easy.  He understands the game.  He knows what to do.  The dude’s got a plan!

In a dirty fight Godel would win.  Because he’ll chew on anything that isn’t food.  (snap!)

Posted in -- By the Physicist, April Fools | 8 Comments