Ask a Mathematician / Ask a Physicist

Physicist: The term “Entropy” shows up both in thermodynamics and information theory, so (since thermodynamics called dibs), I’ll call thermodynamic entropy “entropy”, and information theoretic entropy “information”.

I can’t think of a good way to demonstrate intuitively that entropy and information are essentially the same, so instead check out the similarities!  Essentially, they both answer the question “how hard is it to describe this thing?”.  In fact, unless you have a mess of time on your hands, just go with that.  For those of you with some time, a post that turned out to be longer than it should have been:

Entropy!) Back in the day a dude named Boltzmann found that heat and temperature didn’t effectively describe heat flow, and that a new variable was called for.  For example, all the air in a room could suddenly condense into a ball, which then bounces around with the same energy as the original air, and conservation of energy would still hold up.  The big problem with this scenario is not that it violates any fundamental laws, but that it’s unlikely (don’t bet against a thermodynamicist when they say something’s “unlikely”).  To deal with this Boltzmann defined entropy.  Following basic probability, the more ways that a macrostate (things like temperature, wind blowing, “big” stuff with lots of molecules) can happen the more likely it is.  The individual configurations (atom 1 is exactly here, atom 2 is over here, …) are called “microstates” and as you can imagine a single macrostate, like a bucket of room temperature water, is made up of a hell of a lot of microstates.

Now if a bucket of water has 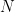microstates, then 2 buckets will have N² microstates (1 die has 6 states, 2 dice have 36 states).  But that’s pretty tricky to deal with, and it doesn’t seem to be what nature is concerned with.  If one bucket has entropy E, you’d like two buckets to have entropy 2E.  Here’s what nature seems to like, and what Bolzmann settled on: E = k log(N), where E is entropy, N is the number of microstates, and k is a physical constant (k is the Boltzmann constant, but it hardly matters, it changes depending on the units used, and the base of the log).  In fact, Boltzmann was so excited about his equation and how well it works that he had it carved into his head stone (he used different letters, so it reads ““, but whatever).  The “log” turns the “squared” into “times 2”, which clears up that problem.  Also, the log can be in any base, since changing the base would just change k, and it doesn’t matter what k is (as long as everyone is consistent).

This formulation of entropy makes a lot of sense.  If something can only happen in one way, it will be unlikely and have zero entropy.  If it has many ways to happen, it will be fairly likely and have higher entropy.  Also, you can make very sensible statements with it.  For example: Water expands by a factor around 1000 when it boils, and it’s entropy increases 1000 fold.  That’s why it’s easy to boil water in a pot (it increases entropy), and it’s difficult to condense water in a pot (it decreases entropy).  You can also say that if the water is in the pot then the position of each molecule is fairly certain (it’s in the pot), so the entropy is low, and when the water is steam then the position is less certain (it’s around here somewhere), so the entropy is high.  As a quick aside, Boltzmann’s entropy assumes that all microstates have the same probability.  It turns out that’s not quite true, but you can show that the probability of seeing a microstate state with a different probability is effectively zero, so they may as well all have the same probability.

Information!) In 1948 a dude named Shannon (last name) was listening to a telegraph line and someone asked him “how much information is that?”.  Then information theory happened.  He wrote a paper worth reading, that can be understood by anyone who knows what “log” is and has some patience.

Say you want to find the combination of a combination lock.  If the lock has 2 digits, there are 100 (10²) combinations, if it has 3 digits there are 1000 (10³) combinations, and so on.  Although a 4 digit code has a hundred times as many combinations as a 2 digit code, it only takes twice as long to describe.  Information is the log of the number of combinations.  So 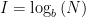where I is the amount of information, N is the number of combinations, and b is the base.  Again, the base of the log can be anything, but in information theory the standard is base 2 (this gives you the amount of information in “bits”, which is what computers use).  Base 2 gives you bits, base e (the natural log) gives you “nats”, and base 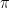gives you “slices”.  Not many people use nats, and nobody ever uses slices (except in bad jokes), so from now on I’ll just talk about information in bits.

So, say you wanted to send a message and you wanted to hide it in your padlock combination.  If your padlock has 3 digits you can store I = log₂(1000) = 9.97 bits of information.  10 bits requires 1024 combinations.  Another good way to describe information is “information is the minimal number of yes/no questions you have to ask (on average) to determine the state”.  So for example, if I think of a letter at random, you could ask “Is it A?  Is it B? …” and it would take 13 questions on average, but there’s a better method.  You can divide the alphabet in half, then again, and again until the letter is found.  So a good series of questions would be “Is is A to M?”, and if the answer is “yes” then “Is it A to G?”, and so on.  It should take log₂(26) = 4.70 questions on average, so it should take 4.7 bits to describe each letter.

In thermodynamics every state is as likely to come up as any other.  In information theory, the different states (in this case the “states” are letters) can have different likelyhoods of showing up.  Right of the bat, you’ll notice that z’s and q’s occur rarely in written English (this post has only 4 “non-Bolzmann” z’s and 16 q’s), so you can estimate that the amount of information in an English letter should be closer to log₂(24) = 4.58 bits.  Shannon figured out that if you have N “letters” and the probability of the first letter is P₁, of the second letter is P₂, and so on, then the information per digit is 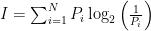.  If all the probabilities are the same, then this summation reduces to I = log₂(N).

As weird as this definition looks, it does makes sense.  If you only have one letter to work with, then you’re not sending any information since you always know what the next letter will be (I = 1 log(1) +0log(0) + … + 0log(0) = 0).  By the same token, if you use all of the letters equally often, it will be the most difficult to predict what comes next (information per digit is maximized when the probability is equal, or spread out, between all the letters).  This is why compressed data looks random.  If your data isn’t random, then you could save room by just describing the pattern.  For example: “ABABABABABABABABABAB” could be written “10AB”.  There’s an entire science behind this, so rather than going into it here, you should really read the paper.

Overlap!) The bridge between information and entropy lies in how hard it is to describe a physical state or process.  The amount of information it takes to describe something is proportional to its entropy.  Once you have the equations (“I = log₂(N)” and “E = k log(N)”) this is pretty obvious.  However, the way the word “entropy” is used in common speech is a little misleading.  For example, if you found a book that was just the letter “A” over and over, then you would say that it had low entropy because it’s so predictable, and that it has no information for the same reason. If you read something like Shakespeare on the other hand, you’ll notice that it’s more difficult to predict what will be written next.  So, somewhat intuitively, you’d say that Shakespeare has higher entropy, and you’d definitely say that Shakespeare has more information.

As a quick aside, you can extend this line of thinking empirically and you’ll find that you can actually determine if a sequence of symbols is random, or a language, etc.  It has been suggested that an entropy measurement could be applied to post modernist texts to see if they are in fact communicating anything at all (see “Sokal affair“).  This was recently used to demonstrate that the Indus Script is very likely to be a language, without actually determining what the script says.

In day to day life we only describe things with very low entropy.  If something has very high entropy, it would take a long time to describe it so we don’t bother.  That’s not a indictment of laziness, it’s just that most people have better things to do than count atoms.  For example: If your friend gets a new car they may describe it as “a red Ferrari 250 GT Spyder” (and congratulations).  The car has very little entropy, so that short description has all the information you need.  If you saw the car you’d know exactly what to expect.  Later it gets dented, so they would describe it as “a red Ferrari 250 GT Spyder with a dent in the hood”.

Easy to describe, and soon-to-be-difficult to describe.

As time goes on and the car’s entropy increases, and it takes more and more information to accurately describe the car.  Eventually the description would be “scrap metal”.  But “scrap metal” tells you almost nothing.  The entropy has gotten so high that it would take forever to effectively describe the ex-car, so nobody bothers to try.

By the by, I think this post has more information than any previous post.  Hence all the entropy.