Physicist: Normal gravity on Earth, , never changes. However, the acceleration,
, due to centrifugal force on the station is given by
, where
is how fast the station is spinning, and R is the radius of the station. If you’re sitting still or walking slowly on a space station, then you’d probably never notice the difference, but if you run either with or against the direction of spin you can change the value of
(for yourself), and thus change the amount of centrifugal force you experience. Whether or not you notice a difference now depends on how big the station is.

Kick-ass, spinning space station (from "2001")
The acceleration, due to gravity on the surface of the Earth is about , and I would guess that a
change in your weight is generally detectable. Given this
estimate, a running speed of around
(10 mph), and assuming that the station is spinning exactly fast enough to have
, then, after some math happens, you’ll find that when the radius of the station is less than around 3.25 km that you can detect the difference. So, you could tell the difference on any ship or station likely to be made in this solar system at least.
If you don’t feel like running back and forth you can try playing catch. You’ll find that when you throw a ball spinward that it curves down, and that when you throw the ball anti-spinward it curves up. In fact, if you can throw the ball as fast as the station spins, then you can make the ball fly at the same height forever (assuming no air resistance). In this case the ball is actually sitting still while the station spins around it.
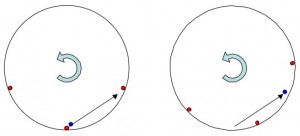
Throwing a ball spinward causes it to fall short
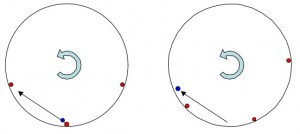
Throwing a ball anti-spinward causes it to go farther